Từ đỉnh một tháp cao 180m, người ta ném một quả cầu theo phương ngang với vận tốc ban đầu v0. Sau 4 giây vận tốc của quả cầu hợp với phương ngang một góc 300.
a. Tính vận tốc ban đầu của quả cầu? Thời gian vật chạm đất?
b. Viết phương trình quỹ đạo của quả cầu?
c. Vận tốc mà nó chạm đất? Tính góc mà vận tốc hợp với phương nằm ngang khi chạm đất?


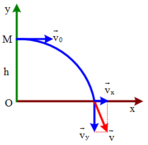
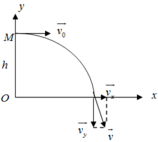
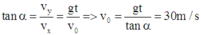
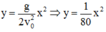
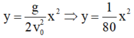

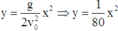
Chọn gốc tọa độ tại mặt đất.
\(v_0\) là vận tốc ban đầu vật.
\(Ox:\left\{{}\begin{matrix}v_x=v_0=hằngsố\\x=v_0\cdot t\end{matrix}\right.\)
\(Oy:\left\{{}\begin{matrix}v_y=g\cdot t\\y=h-\dfrac{1}{2}gt^2\end{matrix}\right.\)
Tại thời điểm \(t=4a;\alpha=30^o\)\(\Rightarrow v_x=v_y\)
\(\Rightarrow v_0=g\cdot t=10\cdot4=40\)m/s
Thời gian vật chạm đất\(\left(y=0\right)\)
\(\Rightarrow h-\dfrac{1}{2}gt^2=0\Rightarrow h=\dfrac{1}{2}gt^2\)
\(\Rightarrow t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot180}{10}}=6s\)
Phương trình quỹ đạo của quả cầu:
\(y=\dfrac{g}{2v_0^2}\cdot x^2=\dfrac{10}{2\cdot40^2}\cdot x^2=\dfrac{x^2}{320}\)
Vận tốc khi chạm đất:
\(v=\sqrt{v^2_0+\left(g\cdot t\right)^2}=\sqrt{40^2+\left(10\cdot4\right)^2}=40\sqrt{2}\)m/s
Khi đó góc tính đc:
\(v^2=v^2_0+\left(g\cdot t\right)^2=\left(v_0\cdot cos\beta\right)^2\)
\(\Rightarrow v=v_0\cdot cos\beta\Rightarrow cos\beta=\dfrac{v}{v_0}=\dfrac{40\sqrt{2}}{40}=\sqrt{2}\)
Hơi vô lí