Tìm abcd biết abcd+abc+abd=4426
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 2 2020
\(1000a+100b+10c+d+100a+10b+c+100a+10b+d=4426\)
\(\Leftrightarrow1200a+120b+11c+2d=4426\)
\(\Rightarrow1200a< 4426\Rightarrow a\le3\)
Nếu \(a\le2\Rightarrow1200a+120b+11c+2d\le1200.2+9\left(120+11+2\right)=3597< 4426\left(ktm\right)\)
\(\Rightarrow2< a\le3\Rightarrow a=3\)
\(\Rightarrow120b+11c+2d=4426-1200.3=826\)
- Nếu \(b\ge7\Rightarrow120b\ge840>826\left(ktm\right)\) \(\Rightarrow b< 7\)
Nếu \(b\le5\Rightarrow120b+11c+2d\le120.5+9.\left(11+2\right)=717< 826\left(ktm\right)\)
\(\Rightarrow5< b< 7\Rightarrow b=6\)
\(\Rightarrow11c+2d=826-120.6=106\)
Lý luận tương tự ta được \(c>7\)
Mà \(2d\) và \(106\) chẵn \(\Rightarrow c\) chẵn \(\Rightarrow c=8\Rightarrow d=9\)
Vậy số cần tìm là \(3689\)
NH
3
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2021
Tam giác ABD cân tại D, mà \(\Delta ABC=\Delta ABD\)
\(\Rightarrow\Delta ABC\) cân tại C với \(AC=BC=2a\) và \(\widehat{ACB}=120^0\)
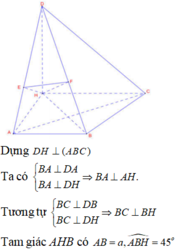
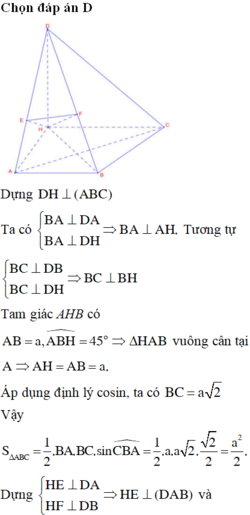
Gọi H là trung điểm AB \(\Rightarrow DH\perp\left(ABC\right)\)
\(DH=2a.cos60^0=a\)
Dựng trung trực của AC cắt CH kéo dài tại O
\(\Rightarrow OC=\dfrac{AC}{2.cos60^0}=2a\)
Đồng thời \(\Rightarrow OA=OB=OC=OD\Rightarrow O\) là tâm mặt cầu ngoại tiếp tứ diện
\(\Rightarrow R=2a\Rightarrow S=4\pi R^2=16\pi a^2\)
a = 3
b = 6
c = 8
d = 9
a=3 b=6 c=8 d=9