cho đường tròn (O) đường kính AB. lấy điểm A tuộc đường tròn (O) (A # B,C) trên cùng 1 nửa mặp phẳng bờ BC chứa điểm A tiếp tuyến Bx của đường tròn ( O) cắt CA tại d. từ D kẻ tiếp tuyến DE với đường tròn (O) (E là trung điểm) gọi I là giao điểm của OD và BEa) Chứng minh OD vuông góc với BE và DI.DO = DA.DCb) Kẻ AH vuông góc với BC tại H, EH cắt CD tại G. Chứng minh IG song song với...
Đọc tiếp
cho đường tròn (O) đường kính AB. lấy điểm A tuộc đường tròn (O) (A # B,C) trên cùng 1 nửa mặp phẳng bờ BC chứa điểm A tiếp tuyến Bx của đường tròn ( O) cắt CA tại d. từ D kẻ tiếp tuyến DE với đường tròn (O) (E là trung điểm) gọi I là giao điểm của OD và BE
a) Chứng minh OD vuông góc với BE và DI.DO = DA.DC
b) Kẻ AH vuông góc với BC tại H, EH cắt CD tại G. Chứng minh IG song song với BC
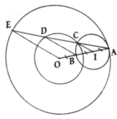
sửa đề : cho BC là đường kính, Kẻ tiếp tuyến DE với E là tiếp điểm bạn nhé
a, Vì DE là tiếp tuyến (O) với E là tiếp điểm => ^OED = 900
Do DE = DB ( tc tiếp tuyến cắt nhau )
OE = OB = R
Vậy DO là trung trực đoạn EB => DO vuông EB
Xét tam giác OED vuông tại E, đường cao EI
Ta có : \(ED^2=DI.DO\)( hệ thức lượng ) (1)
Xét tam giác EDC và tam giác ADE ta có :
^D _ chung
^ECD = ^AED ( góc tạo bởi tiếp tuyến DE và dây cung EA và góc nt chắn cung EA )
Vậy EDC ~ tam giác AED ( g.g )
\(\frac{ED}{AD}=\frac{DC}{ED}\Rightarrow ED^2=DC.AD\)(2)
Từ (1) ; (2) suy ra : \(DC.AD=DI.DO\)