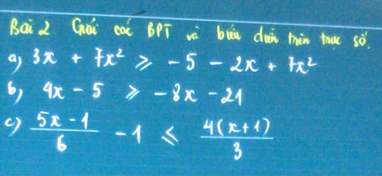Nhờ các bạn giúp bài này với ạ.
Cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
1
16 tháng 2 2022
a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)
11 tháng 4 2021
A=\(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+....+\dfrac{1}{49}-\dfrac{1}{50}\)
=\(\dfrac{1}{1}-\dfrac{1}{50}\)=\(\dfrac{49}{50}\)
TT
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 2 2023
Mỗi giờ làm chung, hai bạn làm được:
1:7= 1/7 (công việc)
Lượng việc Tâm phải làm 1 mình là:
1 - 5 x 1/7 = 2/7 (công việc)
Mỗi giờ Tâm làm 1 mình được:
2/7 : 6= 1/21 (công việc)
Nếu làm 1 mình, để hoàn thành công việc Tâm mất:
1 : 1/21= 21(giờ)
1 giờ làm 1 mình thì Thành làm được:
1/7 - 1/21= 2/21(công việc)
Nếu làm 1 mình, để hoàn thành công việc Thành mất:
1: 2/21= 10,5(giờ)
JW
1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2022
Nửa chu vi hình chữ nhật:14 cm
Gọi chiều dài hình chữ nhật là x (cm) với \(7< x< 14\)
Chiều rộng hình chữ nhật là: \(14-x\) (cm)
Diện tích ban đầu của hình chữ nhật: \(x\left(14-x\right)\)
Chiều dài hình chữ nhật sau khi tăng 1cm: \(x+1\)
Chiều rộng sau khi tăng 2cm: \(14-x+2=16-x\)
Diện tích lúc sau: \(\left(x+1\right)\left(16-x\right)\)
Do diện tích tăng lên 25 \(cm^2\) nên ta có pt:
\(\left(x+1\right)\left(16-x\right)-x\left(14-x\right)=25\)
\(\Leftrightarrow x+16=25\)
\(\Leftrightarrow x=9\left(cm\right)\)
Vậy hình chữ nhật ban đầu dài 9cm và rộng 5cm
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
28 tháng 7 2021
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
M
0