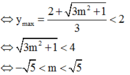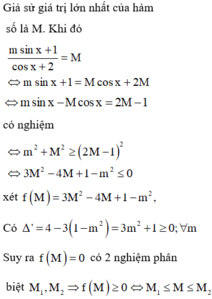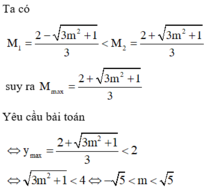tìm tích của các số nguyên lớn hơn -99 và nhỏ hơn 10
tích của 2 số nguyên có 2 chữ số phân biệt giá trị lớn nhất là bao nhiêu
cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
8 tháng 9 2021
Lời giải:
Giả sử nhóm trên có $m$ số nguyên dương phân biệt thỏa mãn, xếp theo thứ tự tăng dần là $a_1,a_2,....,a_m$
Ta có:
$a_1=\frac{2}{3}.\frac{a_1+a_2+....+a_m}{m}$
$3ma_1=2(a_1+a_2+....+a_m)$
$\geq 2[a_1+(a_1+1)+(a_1+2)+....+(a_1+m-2)+3a_1]$
$=2[(m+2)a_1+\frac{(m-1)(m-2)}{2}]=(2m+4)a_1+(m-1)(m-2)$
$\Rightarrow a_1(m-4)\geq (m-1)(m-2)$
Vì $m\geq 2$ nên $m-4\geq 0$
$a_1=\frac{a_m}{3}< \frac{36}{3}=12$
$\Rightarrow a_1\leq 11$
$\Rightarrow 11(m-4)\geq (m-1)(m-2)$
$\Leftrightarrow m^2-14m+46\leq 0$
$\Leftrightarrow -\sqrt{3}+7\leq m\leq \sqrt{3}+7$
Mà $m$ nguyên nên 6\leq m\leq 8$
Vậy $m_{\max}=8$
Ta sẽ chỉ ra bộ số thỏa mãn:
$(11,12,13,14,15,16,18,33)$
CM
21 tháng 5 2017
Đáp án A
Giả sử giá trị lớn nhất của hàm số là M. Khi đó
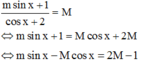
có nghiệm
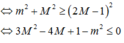
xét 
Có 
Suy ra 
có 2 nghiệm phân biệt
Ta có
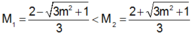
suy ra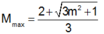 
Yêu cầu bài toán
NT
0