15x2 + 30 = 0
(2x – 1 )2 .4 = 1
Tìm giá trị của x?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


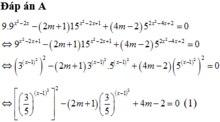

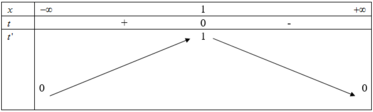
Dựa vào bảng biến thiên hàm f(x), ta thấy để phương trình (1) có 2 nghiệm thực x phân biệt thì phương trình (2) phải có duy nhất 1 nghiệm thuộc khoảng (0;1), nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao điểm của đồ thị hàm số y = 3 5 x - 1 2 và đường thẳng y = 2 m - 1 nên điều kiện của m thỏa mãn là 0 < 2 m - 1 < 1 ⇔ 1 2 < m < 1

1,a, \(\left(2x+1\right)\left(4x^2-2x+1\right)-8x\left(x^2+2\right)=17\)
\(\Leftrightarrow8x^3+1-8x^3-16x=17\)
\(\Leftrightarrow-16x=16\)
\(\Leftrightarrow x=-1\)
\(b,x^2-2x+5\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)+5\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=2\end{cases}}}\)
2,\(M=x^2+2x+6=x^2+2x+1+5=\left(x+1\right)^2+5\ge5\)
Dấu "=" xảy ra <=> x + 1 = 0
<=> x = -1
Vậy \(M_{min}=5\Leftrightarrow x=-1\)

Ta có: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)
\(\Leftrightarrow-4x-3+5x+2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1

\(2x+y=1\Leftrightarrow y=1-2x\\ A=2x^2-y^2=2x^2-\left(1-2x\right)^2\\ A=2x^2-1+4x-4x^2=-2x^2+4x-1\\ A=-2\left(x^2-2x+1\right)+1=-2\left(x-1\right)^2+1\le1\\ A_{max}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1-2\cdot1=-1\end{matrix}\right.\)

Ta có : E = 2x4 + 3x2 + 7
Mà : 2x4 \(\ge0\forall x\in R\)
3x2 \(\ge0\forall x\in R\)
Nên : E = 2x4 + 3x2 + 7 \(\ge7\forall x\in R\)
Vây GTNN của E = 7
Dấu "=" sảy ra khi : \(\hept{\begin{cases}2x^4=0\\3x^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x^4=0\\x^2=0\end{cases}\Leftrightarrow}x=0}\)

Bài 1:
a) \(A=-\left(2x-5\right)^2+6\left|2x-5\right|+4=-\left[\left(2x-5\right)^2-6\left|2x-5\right|+9\right]+13=-\left(\left|2x-5\right|-3\right)^2+13\le13\)
\(maxA=13\Leftrightarrow\) \(\left[{}\begin{matrix}2x-5=3\\2x-5=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\)
b) \(B=-x^2-y^2+2x-6y+9=-\left(x^2-2x+1\right)-\left(y^2+6y+9\right)+19=-\left(x-1\right)^2-\left(y+3\right)^2+19\le19\)
\(maxC=19\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
Bài 2:
\(A=2\left(x^3-y^3\right)-3\left(x+y\right)^2=2\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)=4\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)=x^2-2xy+y^2=\left(x-y\right)^2=2^2=4\)
bài 2
\(A=2\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)\)
\(A=2.2\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)\)
\(A=\left(4x^2+4xy+4y^2\right)+\left(-3x^2-6xy-3y^2\right)\)
\(A=x^2-2xy+y^2=\left(x-y\right)^2=2^2=4\)

vì x+y=4 nền (x+y)^2=4^2 =x^2+ 2xy+y^2=16 ma xy=5 nên 2xy=10 ta có x^2+y^2+10=16 ; x^2+y^2= 16-10 x^2+y^2=6 kết quả mik là z đó nhưng k biết có đúng k bn ak
\(15x^2+30=0\\ \Rightarrow x^2+2=0\left(vô.lí\right)\\ \Rightarrow x\in\varnothing\)
\(\left(2x-1\right)^2.4=1\\ \Rightarrow\left(2x-1\right)^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}2x-1=\dfrac{1}{2}\\2x-1=-\dfrac{1}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)