cho hình vẽ Biết AB//CD A B D c AB=CDA) chứng minh ΔABC=ΔCDBB) chứng minh AD=BCC) chứng minh...
Đọc tiếp
cho hình vẽ
Biết AB//CD
AB=CD
A) chứng minh ΔABC=ΔCDB
B) chứng minh AD=BC
C) chứng minh AD//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 5 2021
a) Ta có :góc ABD = góc BDC (1)(2 góc so le trong của AB//CD)
góc IAB+gócABD=90 độ (tam giác IABvuông tại I)
lại có góc BDC+ góc DBC=90(do tam giác BDC vuông tại C)
mà ABD=BDC (Chứng minh trên)=> IAB=DBC(2)
Từ (1) và (2)=> tam giác IBA đồng dạng tam giác CDB
b) tam giác BDA vuông tại A đường cao AI nên ta có:
DI*DB=AD2mà AD=BC(ABCD là hình chữ nhật) nên DI*DB=BC2
25 tháng 5 2021
c) ta có: DB*IB=AB2(hệ thức lượng trong tam giác vuông ABD)
mà AB=CD nên DB*DI=CD2
d) lại áp dụng hệ thức lượng trong tam giác ADB ta có: AI*DB=AD*AB
mà AB=CD;AD=BC nên BC*CD=AI*BD
NT
1
ST
2
NB
8 tháng 3 2022
hình e tự vẽ
a) xét tg ABD vuông tại D
\(\Rightarrow BD^2=AB^2-AD^2=6^2-4,8^2\\ \Rightarrow BD=\sqrt{6^2-4,8^2}=3,6cm\)
xét tg ADC vuông tại D
\(\Rightarrow AC^2=AD^2+DC^2\\ \Rightarrow AC=\sqrt{4,8^2+6,4^2}=\sqrt{64}=8cm\)
b) có BC =BD+DC==3,6+6,4=10cm
mà \(10^2=6^2+8^2\\ \Leftrightarrow BC^2=AB^2+AC^2\)
=> tg ABC vg tại A
bài này chủ yếu dùng pytago thôi áp dụng vào là làm dễ
29 tháng 6 2016
ta có : AB//CD và AD//BC
=> ABCD là hình bình hành
=>theo tính chất hình bình hành thì AB=CD VÀ BD = AD
B) nếu O là giao hai đường chéo thì mới làm dduocj
theo tính chất hình bình hành thì hai đường chéo giao nhau tại trung điểm mỗi đường
=> OC=OA và OB=OD
CM
1 tháng 11 2017
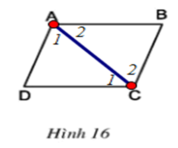
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
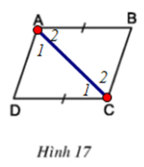
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
AT
18 tháng 11 2016
1) Ta có hình vẽ sau:
Vì AB // CD nên \(\widehat{A_1}\) = \(\widehat{C_1}\) (so le trong)
AD // BC nên \(\widehat{A_2}\) = \(\widehat{C_2}\) ( so le trong)
Xét ΔABC và ΔCDA có:
\(\widehat{A_1}\) = \(\widehat{C_1}\) (cm trên)
AC: Cạnh chung
\(\widehat{A_2}\) = \(\widehat{C_2}\) (cm trên)
\(\Rightarrow\) ΔABC = ΔCDA (g.c.g) (đpcm)
2) Chứng minh tương tự ta có: ΔCDA = ABC (g.c.g)
\(\Rightarrow\) AB = CD ( 2 cạnh tương ứng) (đpcm)
3) Mình sửa lại chỗ AE = AC là AE = AB đó nha, bn ghi nhầm đề!!!
Ta có hình vẽ sau:
Xét ΔABC và ΔAFE có:
AE = AB (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)
AF = AC (gt)
\(\Rightarrow\) ΔABC = ΔAFE(c.g.c) (đpcm)
18 tháng 11 2016
Bạn áp dụng trường hợp bằng nhau cạnh - góc - cạnh của tam giác rồi chứng minh nha
b: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó:ABCD là hình bình hành
Suy ra: AD=BC