lập phương trình bậc hai có hai nghiệm x1, x2 thỏa mãn
4x1x2-5(x1+x2)+4=0
(x1-1)(x2-1)=1/(m-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để phương trình (1) có nghiệm thì:
\(\Delta'\ge0\Rightarrow\left(m-1\right)^2-\left(2m-5\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-2m+5\ge0\)
\(\Leftrightarrow\left(m-2\right)^2+2\ge0\) (luôn đúng)
Vậy với \(\forall m\) thì phương trình (1) luôn có nghiệm.
Theo định lí Vi-et cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
Ta có: \(x_1< 2< x_2\Rightarrow\left\{{}\begin{matrix}x_1-2< 0\\x_2-2>0\end{matrix}\right.\)
\(\Rightarrow\left(x_1-2\right)\left(x_2-2\right)< 0\)
\(\Rightarrow x_1x_2-2\left(x_1+x_2\right)+4< 0\)
\(\Rightarrow2m-5-2.2\left(m-1\right)+4< 0\)
\(\Rightarrow2m-5-4m+4+4< 0\)
\(\Rightarrow-2m+3< 0\)
\(\Rightarrow m>\dfrac{3}{2}\)

bạn đăng tách ra cho mn giúp nhé
a, Để pt có 2 nghiệm pb
\(\Delta'=1-m\ge0\Leftrightarrow m\le1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\left(1\right)\\x_1x_2=m\left(2\right)\end{matrix}\right.\)
\(x_1-3x_2=0\)(3)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_1=-2\\x_2=-2-x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Thay vào (2) ta được \(m=\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)=\dfrac{3}{4}\)
\(b,\Delta=\left(m+5\right)^2-4\left(-m+6\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-7-4\sqrt{3}\\m\ge-7+4\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x1+x2=m+5\\2x1+3x2=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x1+2x2=2m+10\\2x1+3x2=13\end{matrix}\right.\)\(\)
\(\Rightarrow x2=13-2m-10=3-2m\Rightarrow x1=m+5-x2=m+5-3+2m=3m+2\)
\(x1x2=6-m\Rightarrow\left(3-2m\right)\left(3m+2\right)=6-m\Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=1\left(tm\right)\end{matrix}\right.\)
\(c,\Delta'=\left(m+1\right)^2-\left(m^2-2m+29\right)\ge0\Leftrightarrow m\ge7\)
\(\Rightarrow\left\{{}\begin{matrix}x1+x2=2m+2\\x1=2x2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x2=\dfrac{2m+2}{3}\\x1=\dfrac{2\left(2m+2\right)}{3}\end{matrix}\right.\)
\(\Rightarrow x1.x2=\dfrac{\left(2m+2\right).2\left(2m+2\right)}{9}=m^2-2m+29\Leftrightarrow\left[{}\begin{matrix}m=11\left(tm\right)\\m=23\left(tm\right)\end{matrix}\right.\)

\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)

a: \(\text{Δ}=\left(-m\right)^2-4\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)
để phương trình có hai nghiệm phân biệt thì m-2<>0
hay m<>2
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1-x_2=5\\x_1x_2=m-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x_1=m+5\\x_2=x_1-5\\x_1x_2=m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+5}{2}\\x_2=\dfrac{m+5}{2}-5=\dfrac{m-5}{2}\\x_1x_2=m-1\end{matrix}\right.\)
\(\Leftrightarrow m^2-25=4m-4\)
\(\Leftrightarrow m^2-4m-21=0\)
=>(m-7)(m+3)=0
=>m=7 hoặc m=-3

Giả sử x 1 , x 2 la hai nghiệm của phương trình x 2 + px + q = 0
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - p/1 = - p; x 1 x 2 = q/1 = q
Phương trình có hai nghiệm là x 1 + x 2 và x 1 x 2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x 2 - qx + px - pq = 0 ⇔ x 2 + (p - q)x - pq = 0
Phương trình cần tìm: x 2 + (p - q)x - pq = 0

Hai số 1 - 2 và 1 + 2 là nghiệm của phương trình :
[x – (1 - 2 )][x – (1 + 2 )] = 0
⇔ x 2 – (1 + 2 )x – (1 - 2 )x + (1 - 2 )(1 + 2 ) = 0
⇔ x 2 – 2x – 1 = 0

Phương trình x 2 – 2(m – 2)x + 2m – 5 = 0 có a = 1 ≠ 0 và
∆ ' = ( m − 2 ) 2 – 2 m + 5 = m 2 – 6 m + 9 = ( m – 3 ) 2 ≥ 0 ; ∀ m
Nên phương trình luôn có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = 2 m − 4 x 1 . x 2 = 2 m − 5
X é t x 1 ( 1 − x 2 ) + x 2 ( 2 – x 1 ) < 4 ⇔ ( x 1 + x 2 ) – 2 x 1 . x 2 − 4 < 0
⇔ 2m – 4 – 2(2m – 5) – 4 < 0 ⇔ −2m + 2 < 0 m > 1
Vậy m > 1 là giá trị cần tìm
Đáp án: A

c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: 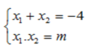
Ta có: x 1 2 + x 2 2 = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10
⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: x 1 2 + x 2 2 = 10