cho tam giác abc=tam giác def có ab=3cm,df=4cm,ef=5cm.tính chu vi của mỗi tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2022
Bài 3:
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên \(\widehat{BAD}=\widehat{CAD}\)
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
AN
29 tháng 12 2021
Xét tam giác ABC:
BC=EF=5cm
=> Chu vi của tam giác ABC là:
AB+AC+BC=3+4+5=12(cm)
Xét tam giác DEF:
AB=DE=3cm
AC=DF=4cm
=> Chu vi tam giác DEF là:
DE+DF+EF=3+4+5=12
Vậy chu vi tam giác ABC: 12(cm)
Chu vi tam giác DEF:12(cm)
HD
2
22 tháng 7 2017
Vì tam giác ABC = tam giác DEF => AB = DE,BC =EF, AC = DF. Vậy chu vi của tam giác DEF = 3+4+6 =13cm.
7 tháng 12 2018
Ta có:tam giác ABC = tam giác DEF (gt)
\(\Rightarrow\)AB = DE
AC = DF
BC = EF
Mà theo đề ta có : AB = 3cm \(\rightarrow\) DE =3cm ; AC = 4cm \(\rightarrow\)DF =4cm ; EF = 6cm\(\rightarrow\)BC = 6cm
nên ta có chu vi của tam giác ABC là:
AB + AC + BC = 3 + 4 + 6 = 13 (cm)
Vì tam giác ABC = tam giác DEF
Do đó: tam giác DEF có chu vi là : 13 (cm)
26 tháng 1 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{3}=\dfrac{AC}{5}=\dfrac{BC}{7}=\dfrac{AB+BC+CA}{3+5+7}=\dfrac{20}{15}=\dfrac{4}{3}\)
Do đó: AB=4(cm); AC=20/3(cm); BC=28/3(cm)
OP
26 tháng 1 2022
D E F A B C
ta có:\(\dfrac{DE}{AB}=\dfrac{DF}{AC}=\dfrac{EF}{BC}\)
\(\Leftrightarrow\dfrac{3}{AB}=\dfrac{5}{AC}=\dfrac{7}{BC}\)
áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{3+5+7}{AB+AC+BC}=\dfrac{15}{20}=\dfrac{3}{4}\)
<=>\(\dfrac{AB+AC+BC}{DE+EF+DF}=\dfrac{4}{3}\)
<=>AB=\(\dfrac{4}{3}.DE=\dfrac{4}{3}.3=4\)
AC=\(\dfrac{4}{3}.DF=\dfrac{4}{3}.5=\dfrac{20}{3}\)
BC=\(\dfrac{4}{3}.EF=\dfrac{4}{3}.7=\dfrac{28}{3}\)
VẬY...
HT
1
17 tháng 11 2021
ΔABC=DEFΔABC=DEF
=> AB=DE=3cm; BC=EF=5cm; AC=DF=4cm.
Diện tích ΔABCΔABC=Diện tích ΔDEFΔDEF=3+5+4=12 (cm)
Đ/S:12
ai k mik 3 cái mik k lại 9 cái
#mai
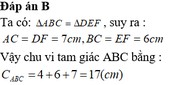
\(\Delta ABC=\Delta DEF\Rightarrow AB=DE;AC=DF;BC=EF\\ \Rightarrow P_{ABC}=P_{DEF}=AB+AC+BC=AB+DF+EF=12\left(cm\right)\)