Cho Hình chóp SABCD có ABCD là một tú giác lồi. Gọi M,N lần lượt là trung điểm của SA và Sc.
Xác định thiết diện của hình chóp khi cắt bởi các mặt phẳng lần lượt qua M, N và// với mp (SBD)
b/ Gọi I và J lần lượt là giao điểm của AC với ha mặt phẳng nói trên. Chứng minh AC= 2IJ

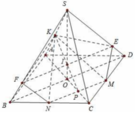
a. Qua M kẻ đường thẳng song song SB cắt AB tại E
Qua M kẻ đường thẳng song song SD cắt AD tại H
\(\Rightarrow\Delta MEH\) là thiết diện của mp qua M và song song (SBD)
Qua N kẻ đường thẳng song song SB cắt BC tại F
Qua N kẻ đường thẳng song song SD cắt CD tại G
\(\Rightarrow NFG\) là thiết diện của mp qua N và song song (SBD)
b. Gọi O là giao điểm AC và BD
Do M là trung điểm SA, \(ME||SB\Rightarrow ME\) là đường trung bình tam giác SAB
\(\Rightarrow\) E là trung điểm AB
Hoàn toàn tương tự, ta có F là trung điểm BC, G là trung điểm CD, H là trung điểm AD
\(\Rightarrow EH\) là đường trung bình tam giác ABD, FG là đtb tam giác BCD
\(\Rightarrow I\) là trung điểm AO, J là trung điểm CO
\(\Rightarrow\left\{{}\begin{matrix}OI=\dfrac{1}{2}OA\\OJ=\dfrac{1}{2}OC\end{matrix}\right.\) \(\Rightarrow OI+OJ=\dfrac{1}{2}\left(OA+OC\right)\Rightarrow IJ=\dfrac{1}{2}AC\)