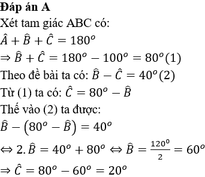Tam giác ABC có góc A = 40o; các đường cao cắt nhau tại H. Khi đó số đo góc BHC bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


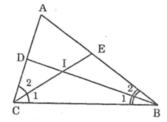
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C

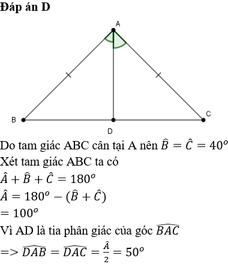
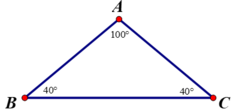
Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có:
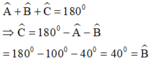
Suy ra ∆ABC cân tại A.

Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.

Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A

Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A

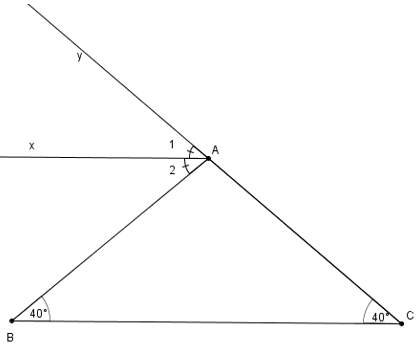
Ta có: BAy=B+C (góc ngoài của tam giác)
BAy=400+400=800
Ax là p/g của BAy
⇒ A1=A2=400
Ta có: A2=B=400
Mà hai góc này ở vị trí SLT
⇒ BC//Ax
Ta có: BAy=B+C (góc ngoài của tam giác)
BAy=400+400=800
Ax là p/g của BAy
⇒ A1=A2=400
Ta có: A2=B=400
Mà hai góc này ở vị trí SLT
⇒ BC//Ax

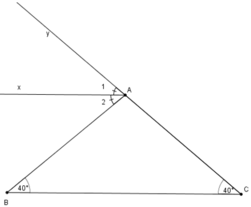
Gọi góc BAy là góc ngoài của tam giác ABC

Mà hai góc này ở vị trí so le trong nên Ax//BC (đpcm).

Ta có ∠C = 180o - 80o - 40o = 60o
Vì CI là tia phân giác của góc C nên ∠(ACI) = 60o : 2 = 30o. Chọn D