a. Cho 2 phân số bằng nhau a / b va c/ d. Chứng tỏ ab=cd
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) a − b = a . ( − 1 ) − b . ( − 1 ) = − a b
b) − a − b = − a . ( − 1 ) − b . ( − 1 ) = a b

#)Giải :
Ta có : \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}=\frac{a^2-b^2}{c^2-d^2}\)
\(\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\left(đpcm\right)\)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\)(1)
Ta có : \(ab\left(c^2-d^2\right)=abc^2-abd^2=acbc-adbd\)(2)
\(cd\left(a^2-b^2\right)=a^2cd-b^2cd=acad-bcbd\)(3)
Từ (1),(2),(3) => \(ab\left(c^2-d^2\right)=cd\left(a^2-b^2\right)\Rightarrow\text{đpcm}\)


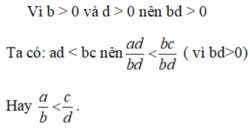
Theo bài ra ta có:
a/b=c/d
<=>ad/bd=bc/bd
<=>ad=bc
bn xem lại đề