Giúp em với🤧
Cảm ơn trước ạ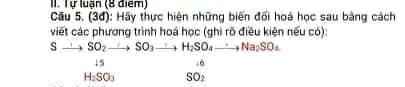
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 3:
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)
\(\widehat{ACN}+\widehat{ACB}=180^0\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
Xét ΔAMN có AM=AN
nên ΔAMN cân tại A


Câu 4:
Gọi chiều rộng là x
Chiều dài là 2x+9
Theo đề, ta có phương trình: x(2x+9)=200
\(\Leftrightarrow2x^2+9x-200=0\)
\(\Delta=9^2-4\cdot2\cdot\left(-200\right)=881>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-9-29}{4}=\dfrac{-38}{4}\left(loại\right)\\x_2=\dfrac{-9+29}{4}=5\left(nhận\right)\end{matrix}\right.\)
Vậy: CHu vi là (2x+9+x)x2=(15+9)x2=48(m)

a) \(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{19.21}\)
\(A=\dfrac{1}{2}.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
\(A=\dfrac{1}{2}.\left(1-\dfrac{1}{21}\right)\)
\(A=\dfrac{1}{2}.\left(\dfrac{21}{21}-\dfrac{1}{21}\right)\)
\(A=\dfrac{1}{2}.\dfrac{20}{21}\)
\(A=\dfrac{10}{21}\)
b) \(B=\dfrac{1}{99}-\dfrac{1}{99.98}-\dfrac{1}{98.97}-\dfrac{1}{97.96}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
\(B=\dfrac{1}{99}-\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{96.97}+\dfrac{1}{97.98}+\dfrac{1}{98.99}\right)\)
\(B=\dfrac{1}{99}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{96}-\dfrac{1}{97}+\dfrac{1}{97}-\dfrac{1}{98}+\dfrac{1}{98}-\dfrac{1}{99}\right)\)
\(B=\dfrac{1}{99}-\left(1-\dfrac{1}{99}\right)\)
\(B=\dfrac{1}{99}-\left(\dfrac{99}{99}-\dfrac{1}{99}\right)\)
\(B=\dfrac{1}{99}-\dfrac{98}{99}\)
\(B=-\dfrac{97}{99}\)


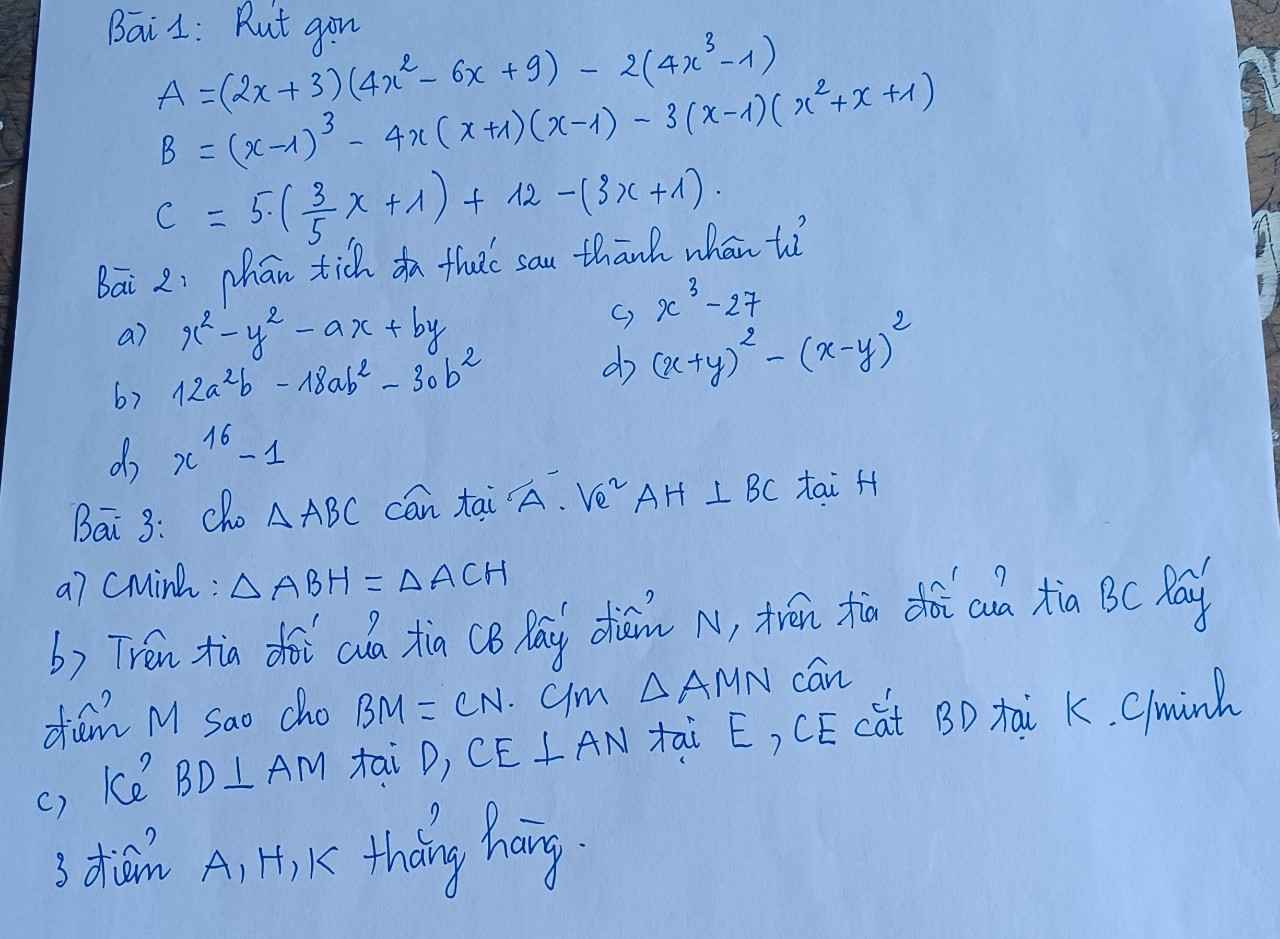






 giúp em với ạ em cảm ơn trước ạ
giúp em với ạ em cảm ơn trước ạ
\(S+O_2\xrightarrow[]{t^o}SO_2\)
\(SO_2+\dfrac{1}{2}O_2\xrightarrow[V_2O_5]{t^o}SO_3\)
\(SO_3+H_2O\rightarrow H_2SO_4\)
\(H_2SO_4+Na_2O\rightarrow Na_2SO_4+H_2O\)
\(SO_2+H_2O⇌H_2SO_3\)
\(2H_2SO_{4\left(đ\right)}+Cu\xrightarrow[]{t^o}CuSO_4+SO_2+2H_2O\)
\(\left(1\right)S+O_2\overset{t^o}{--->}SO_2\)
\(\left(2\right)2SO_2+O_2\xrightarrow[V_2O_5]{t^o}2SO_3\)
\(\left(3\right)SO_3+H_2O--->H_2SO_4\)
\(\left(4\right)H_2SO_4+2NaOH--->Na_2SO_4+2H_2O\)
\(\left(5\right)SO_2+H_2O--->H_2SO_3\)
\(\left(6\right)H_2SO_4+Na_2SO_3--->Na_2SO_4+SO_2\uparrow+H_2O\)