CMR phân số sau bằng...
Đọc tiếp
CMR phân số sau bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KK
1
13 tháng 1 2017
a,ta co (+a).(+b)=(-a).(-b)
nen a/ -b = a /b
b, ta co (+a).(-b)= (+b).(-a)
nen -a/-b=a/b
MH
1
20 tháng 8 2015
\(\frac{4}{n}=\frac{1}{n}+\frac{3}{n}\)
+) Xét n = 3k ( k là số tự nhiên > 1)
\(\frac{4}{n}=\frac{n+1}{n\left(n+1\right)}+\frac{3}{n}=\frac{1}{n+1}+\frac{1}{n\left(n+1\right)}+\frac{3}{n}=\frac{1}{3k+1}+\frac{1}{3k\left(3k+1\right)}+\frac{1}{k}\)
+) Xét n = 3k + 1:
\(\frac{4}{n}=\frac{1}{n}+\frac{3}{n}=\frac{1}{n}+3.\left(\frac{1}{n-1}-\frac{1}{n\left(n-1\right)}\right)=\frac{1}{n}+\frac{3}{n-1}-\frac{3}{n\left(n-1\right)}=\frac{1}{3k+1}+\frac{3}{3k}+\frac{-3}{3k\left(3k+1\right)}=\frac{1}{3k+1}+\frac{1}{k}+\frac{1}{-k\left(3k+1\right)}\)
+) Xét n = 3k + 2:
\(\frac{4}{n}=\frac{1}{n}+\frac{3}{n}=\frac{1}{n}+3.\left(\frac{1}{n+1}+\frac{1}{n\left(n+1\right)}\right)=\frac{1}{n}+\frac{3}{n+1}+\frac{3}{n\left(n+1\right)}=\frac{1}{3k+2}+\frac{1}{k+1}+\frac{1}{\left(3k+2\right).\left(k+1\right)}\)
Vậy Với mọi n > 4 thì 4/ n đều phân tích thành tổng của 3 phân số khác nhau có dạng 1/n
=> đpcm
28 tháng 2 2023
Khẳng định nào sau đây là đúng?
A. hai phân số được gọi đối nhau nếu tổng của chúng bằng 0
B. hai phân số được gọi là đối nhau nếu tổng của chúng bằng 1.
C. hai phân số được gọi là đối nhau nếu tổng của chúng bằng -1
D. hai phân số được gọi là đối nhau nếu tích của chúng bằng 0
→ Chọn A
@Nae
27 tháng 2 2018
a.Ta có :
+) 1/2 = 32/64
+) 1/4 = 16/64
+) 1/8 = 8/64
+) 1/32 = 2/64
=> 32/64 - 16/64 + 8/64 - 2/64 +1/64 = 21/64
+) 21/64 = 21×3/64×3 = 63/192 ; 1/3 = 1×64/3×64 = 64/192
Mà 63/192 < 64/192
Vậy 1/2 - 1/4 + 1/8 - 1/16 + 1/32 - 1/64 < 1/3
☆ phần b đơn giản, bạn tự làm nhé !
PT
1
CM
2 tháng 3 2017
Rút gọn các phân số chưa tối giản để xuất hiện các phân số bằng nhau.
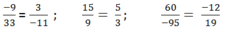
\(\frac{131313}{151515}=\frac{13.10101}{15.10101}=\frac{13}{15}\)
\(\frac{13026}{15030}=\frac{13.1002}{15.1002}=\frac{13}{15}\)
\(\Rightarrowđpcm\)
Ta có: \(\frac{131313}{151515}=\frac{13.10101}{15.10101}=\frac{13}{15}\)
\(\frac{13026}{15030}=\frac{13.1002}{15.1002}=\frac{13}{15}\)
\(\Rightarrow\)\(\frac{131313}{151515}=\frac{13026}{15030}\)( ĐPCM )