A) Cho (o) đường kính 21 cm và đường thẳng a cách o một khoảng bằng 10 cm . Khi đó đường thẳng a và (o)
B) Cho (o) đường kính 30 cm và đường thẳng d cách o một khoảng bằng 15 cm . Khi đó đường thẳng a và (o)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2017
c) Do tam giác ABC nội tiếp đường tròn (O) có AC là đường kính nên tam giác ABC vuông tại B
Khi đó, ta có:
AC2 = AB2 + BC2
CM
22 tháng 4 2018
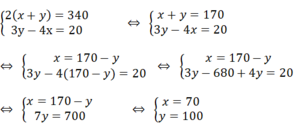
b) Xét tam giác AHO vuông tại H có:
A O 2 = A H 2 + O H 2
⇒ AB = 2AH = 8 (cm)
CM
11 tháng 11 2017
Chọn đáp án D
Phương pháp
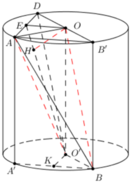
+) Dựng AA’//OO’, BB’//OO’ (A’ thuộc đường tròn (O’) và B’ thuộc đường tròn (O))
+) Xác định khoảng cách giữa OO’ và song song với OB, đưa về bài toán khoảng cách từ điểm đến mặt phẳng.
+) Xác định khoảng cách, áp dụng hệ thức lượng trong tam giác vuông tính khoảng cách.
Cách giải
Dựng AA’//OO’, BB’//OO’ (A’ thuộc đường tròn (O’) và B’ thuộc đường tròn (O))
Ta có:
30 tháng 4 2020
1.Vì đường kính của (O) là 10cm
\(\Rightarrow\) Bán kính của (O) là \(R=\frac{10}{2}=5\)
\(\Rightarrow d\left(O,d\right)=3< R=5\)
\(\Rightarrow d\left(O\right)\)cắt nhau tại 2 điểm phân biệt
2 . Kẻ \(OI\perp AB\Rightarrow I\) là trung điểm AB
Vì \(OI\perp AB\Rightarrow OI=3\Rightarrow AI^2=OA^2-0I^2=5^2-3^2=16\)
\(\Rightarrow AI=4\Rightarrow AB=2AI=8\) vì I là trung điểm AB
3.Vì O, I là trung điểm AC,AB
=> OI là đường trung bình \(\Delta ABC\Rightarrow BC=2OI=6\)
4 . Vì AC là đường kính của (O)
\(\Rightarrow CB\perp AB\Rightarrow CB\perp AM\)
Mà \(CA\perp CM\Rightarrow CB^2=AB.BM\)
\(\Rightarrow BM=\frac{BC^2}{AB}=\frac{6^2}{8}=\frac{9}{2}\)
CM
10 tháng 7 2019
Gọi O là tâm đường tròn, H là chân đường vuông góc hạ từ O đến đường thẳng d
⇒ Độ dài OH là khoảng cách từ O đến đường thẳng d
Ta có: OH = 3cm < R = 5 cm ⇒ d cắt (O) tại 2 điểm phân biệt
a: a và (O) không có điểm chung
b: a và (O) có một điểm chung