4+5+99+32=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)2004100+200499=200499(2004+1)=201499.2005
=>201499.2005chia hết cho 2005
=> 2004100+200499 chia hết cho 2005
b) 413+325-88
=(22)13+(25)5-(23)8
=226+225-224
=224(22+2-1)
=225.5
=>225chia hết cho 5 => 413+325-88 chia hết cho 5


a) (38 - 60) + (20 - 38)
= 38 - 60 + 20 - 38
= (38 - 38) + (-60 + 20)
= 0 - 40
= -40
b) 75 - (20 + 75)
= 75 - 20 - 75
= (75 - 75) - 20
= 0 - 20
= -20
c) 32 + (60 - 32)
= 32 + 60 - 32
= (32 - 32) + 60
= 0 + 60
= 60
d) (81 - 36) - (81 - 36)
= 81 - 36 - 81 + 36
= (81 - 81) + (-36 + 36)
= 0 + 0
= 0
e) (2 + 4 + 6 + 8) - (1 + 3 + 5 + 7)
= 2 + 4 + 6 + 8 - 1 - 3 - 5 - 7
= (2 - 1) + (4 - 3) + (6 - 5) + (8 - 7)
= 1 + 1 + 1 + 1
= 4
f) (1 + 3 + 5 + 7 + ... + 99) - (2 + 4 + 6 + 8 + ... + 100)
= 1 + 3 + 5 + 7 + ... + 99 - 2 - 4 - 6 - 8 - ... - 100
= (1 - 2) + (3 - 4) + (5 - 6) + (7 - 8) + ... + (99 - 100)
= -1 - 1 - 1 - 1 - ... - 1 (50 chữ số 1)
= -50

a) \(2^{2003}\)
Ta có: \(2^{2003}=2^{2000}.2^3=\left(2^4\right)^{500}.8=16^{500}.8=\left(...6\right).8=\left(...8\right)\)
Vậy \(2^{2003}\) có c/s tận cùng là 8.
b) \(4^{99}\)
Ta có: \(4^{99}=4^{98}.4=\left(4^2\right)^{49}.4=16^{49}.4=\left(...6\right).4=\left(...4\right)\)
Vậy \(4^{99}\) có c/s tận cùng là 4.
c) \(9^{99}\)
Ta có: \(9^{99}=9^{98}.9=\left(9^2\right)^{49}.9=81^{49}.9=\left(...1\right).9=\left(...9\right)\)
Vậy \(9^{99}\) có c/s tận cùng là 9.
d) \(7^{99}\)
Ta có: \(7^{99}=7^{96}.7^3=\left(7^4\right)^{24}.\left(...3\right)=\left(...1\right)^{24}.\left(...3\right)=\left(...1\right).\left(...3\right)=\left(...3\right)\)
Vậy \(7^{99}\) có c/s tận cùng là 3.
e) \(8^{99}\)
Ta có: \(8^{99}=8^{96}.8^3=\left(8^4\right)^{24}.\left(...2\right)=\left(...1\right)^{24}.\left(...2\right)=\left(...1\right).\left(...2\right)=\left(...2\right)\)
Vậy \(8^{99}\) có c/s tận cùng là 2.
f) \(789^{5^{7^3}}\)
Ta có: \(5^{7^3}=\left(...5\right)\) lẻ.
Mà 789 có tận cùng 9, 9 khi nâng luỹ thừa bậc lẻ thì có c/s tận cùng là chính nó.
Vậy \(789^{5^{7^3}}\) có c/s tận cùng là 9.
g) \(87^{32}\)
Ta có: \(87^{32}=87^{4.8}=\left(87^4\right)^8=\left(...1\right)^8=\left(...1\right)\)
Vậy \(87^{32}\) có c/s tận cùng là 1.
h) \(58^{33}\)
Ta có: \(58^{33}=58^{32}.58=\left(58^4\right)^8.58=\left(...6\right)^8.58=\left(...6\right).58=\left(...8\right)\)
Vậy \(58^{33}\) có c/s tận cùng là 8.


a) \(S=1^5+3^5+....+75^5+99^5\)
\(\left(2a+1\right)^5-\left(2a+1\right)=2a\left(2a+1\right)\left(2a+2\right)\left[\left(2a+1\right)^2+1\right]\)
\(\left(2a+1\right)^5-\left(2a+1\right)=4a\left(2a+1\right)\left(a+1\right)\left[\left(2a+1\right)^2+1\right]⋮4\)
\(S=\left(1^5-1\right)+\left(3^5-3\right)+....+\left(75^5-75\right)+\left(99^5-99\right)+\left(1+3+5+...+75+99\right)\)
\(\Leftrightarrow\begin{matrix}1^5-1⋮4\\3^5-3⋮4\\5^5-5⋮4\\...........\\75^5-5⋮4\\99^5-99⋮4\end{matrix}\)
\(S_1=1+3+5+7+...+75+99=\frac{\left(1+75\right)\left[\frac{75-1}{2}+1\right]}{2}+99=38.38+96+3\)
\(\Rightarrow S_1:4\) dư 3
\(\Leftrightarrow S\) chia 4 dư 3
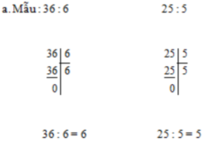
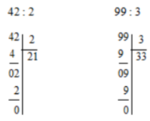
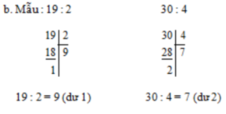
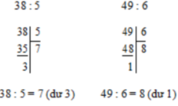

140 nha bn
=140 nha em