1.Tìm x biết x2 - 2xn+1 + 5xn - 4xn+1= 0 (n € N; n # 0)
2.Tìm GTLN của biểu thức \(P=\frac{x^2+y^2+3}{x^2+y^2+2}\)
3.Tổng 3 phân số tối giản bằng \(\frac{325}{63}\) . Các tử tỉ lệ nghịch với 20; 4; 5 .Các mẫu tỉ lệ thuận với 1; 3; 7. Tìm 3 p/số đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
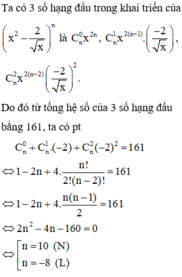
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
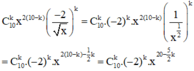
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
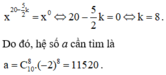

a) \(\frac{n+5}{n+2}=\frac{n+2+3}{n+2}=1+\frac{3}{n+2}\)
\(\Rightarrow n+2\in U\left(3\right)\)
Lập bảng nhé
b)\(\frac{5n+2}{n-1}=\frac{5\left(n-1\right)+7}{n-1}=5+\frac{7}{n-1}\)
\(\Rightarrow n-1\in U\left(7\right)\)
Lập bảng tương tự nhé
c)\(\frac{3n+2}{2n+3}=\frac{3\left(n+3\right)-7}{2\left(n+3\right)-6}=\frac{3}{2}-\frac{7}{2\left(n+3\right)-6}\)
Tương tự nhé
a) Ta có : \(\frac{n+5}{n+2}=\frac{\left(n+2\right)+3}{n+2}=\frac{n+2}{n+2}+\frac{3}{n+2}=1+\frac{3}{n+2}\)
Để n + 5 \(⋮\)n + 2 \(\Leftrightarrow\)\(\frac{3}{n+2}\)\(\in Z\) \(\Leftrightarrow\) 3 \(⋮\) n + 2 \(\Leftrightarrow\)n + 2 \(\in\)Ư ( 3 ) = { -1 ; 1; -3 ; 3 }
* Với n + 2 = 1 => n = 1 - 2 = -1 ( thỏa mãn )
* Với n + 2 = - 1=> n = -1 - 2 = - 3 ( thỏa mãn )
* Với n + 2 = 3 => n = 3 - 2 = 1 ( thỏa mãn )
* Với n + 2 = -3 => n = -3 - 2 = -5 ( thỏa mãn )
Vậy với n \(\in\){ -1; -3; 1; -5 } thì n + 5 \(⋮\)n + 2

\(\dfrac{X}{Y}=\dfrac{7}{5}x^{n-1}-x^{3-n}\)
Để X chia hết cho Y thì n-1>=0 và 3-n>=0
=>1<=n<=3
=>\(n\in\left\{1;2;3\right\}\)
Bài 1: $x$ có thêm điều kiện gì không bạn?
Bài 2:
$P=\frac{x^2+y^2+3}{x^2+y^2+2}=\frac{(x^2+y^2+2)+1}{x^2+y^2+2}=1+\frac{1}{x^2+y^2+2}$
Ta thấy:
$x^2\geq 0; y^2\geq 0$ với mọi $x,y$
$\Rightarrow x^2+y^2+2\geq 2$
$\Rightarrow P\leq 1+\frac{1}{2}=\frac{3}{2}$
Vậy GTNN của $P$ là $\frac{3}{2}$
Giá trị này đạt tại $x^2=y^2=0\Leftrightarrow x=y=0$