Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
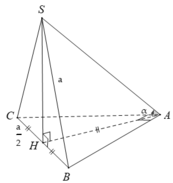
- Gọi H là trung điểm của BC. Suy ra:
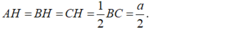
- Ta có:
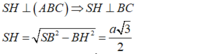
- Do H là hình chiếu của S lên mp(ABC) nên góc giữa đường thẳng SA và mp (ABC) là góc 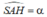
- Xét tam giác vuông SHA có:
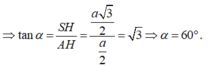

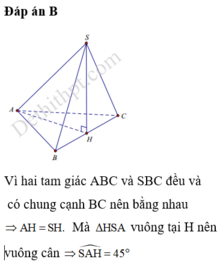
Đáp án B
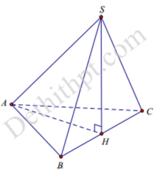
Vì hai tam giác ABC và SBC đều và có chung cạnh BC nên bằng nhau ⇒ A H = S H .
Mà Δ H S A vuông tại H nên vuông cân
⇒ S A H ^ = 45 °

Đáp án là D
Gọi H là trung điểm B C . Ta có A H là hình chiếu vuông góc của S A lên mặt phẳng A B C .
Khi đó S A ; A B C ^ = S A ; A H ^ = S A H ^
Ta có S H = A H S H ⊥ A H ⇒ Δ S A H vuông cân tại - H ⇒ S A H ^ = 45 0 .

Đáp án D
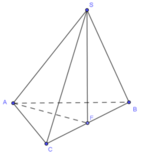
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
![]()
Vậy ![]()

Đáp án D
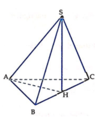
Ta có H là trung điểm của BC, H là hình chiếu của S trên mặt phẳng (ABC) nên HA là hình chiếu của SA trên mặt phẳng (ABC).
Suy ra S A , A B C ^ = S A , H A ^ = S A H ^ .
Lại có Δ A B C = Δ S B C (đều là các tam giác đều cạnh a) nên A H = S H ⇒ Δ S H A vuông cân tại H.
Vậy S A , A B C ^ = S A H ^ = 45 ° .
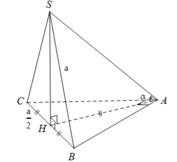
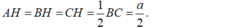
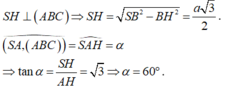
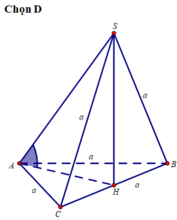

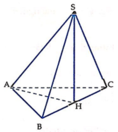

Gọi HH là trung điểm của BCBC suy ra
AH=BH=CH=1\2BC=a\2.
Ta có: SH⊥(ABC)⇒SH=√SB2−BH2=a√3\2
ˆ(SA,(ABC))=ˆ(SA,HA)=ˆSAH=α
⇒tanα=SH\AH=√3⇒α=60∘