Cho tam giác ABC cân tại A. Đường cao AH bằng 1 nửa BC
vậy BAC=....0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
2 tháng 3 2016
AH bằng một nửa BC=>AH=BH=CH=>tam giác BAH=tam giác CAH(2 cạnh góc vuông)=>góc B=góc C
ta có tam giác ABH cân tại H(AH=HB)=>góc BAH= góc B(tính chất tam giác cân)
tương tự=>góc HAC=góc C
góc B=góc C(CMT)
mà góc B=gócBAH
góc C=góc CAH
=>góc BAC=B+C(=BAH+CAH)
mà B=C=>BAC=2B(C) màBAC+B+C=180 độ=>A=180 độ:4=25 độ
ND
2
NN
29 tháng 6 2016
Vì AH bằng một nửa BC=>AH=BH=CH
=>tam giác BAH=tam giác CAH(2 cạnh góc vuông)
=>góc B=góc C
Ta có tam giác ABH cân tại H(AH=HB)
=>góc BAH= góc B(tính chất tam giác cân)
Tương tự ta có: =>góc HAC=góc C
góc B=góc C(CMT)
Mà góc B=góc BAH
góc C = góc CAH
=>góc BAC=B+C(=BAH+CAH)
Mà B=C=>BAC=2B(C) mà BAC+B+C=1800=>A=1800:4=250
Vậy BAC =250
NN
0
BG
1
QQ
3
16 tháng 2 2017
CHÚ Ý: đây là định lý đảo của trung tuyến trong tam giác vuông
Do tam giác ABC cân tại A nên AH là đường cao đồng thời cũng là đường trung tuyến
mà theo ĐL đảo ủa đường trung tuyến thì nếu trung tuyến = một nửa cạnh huyền thì tam giác đó vuông
=> tam giác ABC vuông cân tại A
=> A=90
CM
25 tháng 2 2019
Chú ý H là trực tâm tam giác ABC, từ đó AH vừa là đường cao vừa là đường phân giác
NT
4
22 tháng 8 2015
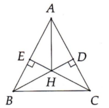
Tam giác vuông ACH có góc C=30độ suy ra CAH=60 độ
Suy ra góc BAC= 120 độ
22 tháng 8 2015
Vì AH = 1/2 BC \(\Rightarrow\)AH là đường trung trực \(\Rightarrow\) H là trung điểm của BC \(\Rightarrow\)AH là đường trung tuyến của \(\Delta\) ABC
Xét \(\Delta\) AHB và \(\Delta\) AHC, có:
AH là cạnh chung
BH=HC ( H là trung điểm BC )
góc AHB = góc AHC ( = 90 độ )
\(\Rightarrow\) \(\Delta\) AHB = \(\Delta\) AHC ( c-g-c)
\(\Rightarrow\)góc ABH = góc ACH
hay góc B = góc C = 30 độ