Tìm số tự nhiên x biết :
e) 0 ⋮ x ; 84 ⋮ x và x > 8.
|
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 7 2019
e) 0 : x = 0
0 chia cho mọi số tự nhiên khác 0 đều bằng 0
nên x ∈ N*
HG
1
3 tháng 11 2019
Ta có: \(12=2^2.3\)
\(40=2^3.5\)
\(\Rightarrow BCNN\left(12;40\right)=2^3.3.5=120\)
\(\Rightarrow x\in\left\{0;120;240;480;...\right\}\)
Vì 0<x<400 nên:
\(\Rightarrow x\in\left\{120;240\right\}\)
^ Học tốt ^
NA
25 tháng 11 2021
a) 20 = 22 . 5
48 = 24 . 3
ƯCLN(20,40) = 22 = 4
ƯC(20,40) = Ư(4) = 1,2,4
Mà theo đề bài 0 < x < 4 nên x = { 1 , 2 }
b) 30 = 2 . 5 . 3
24 = 23 . 3
ƯCLN(30,24) = 2 . 3 = 6
ƯC(30,24) = Ư(6) = 1,2,3,6
Mà theo y/c đề bài 2 < x < 6 nên x = 3
CM
7 tháng 4 2019
a. A = {8}. Vậy tập hợp A có 1 phần tử.
b. B = {0;1;2;…}. Vậy tập hợp B có vô số phần tử.
c. C = {5}. Vậy tập hợp C có 1 phần tử.
d. D = ∅ . Vậy tập hợp D không có phần tử nào.
e. E = {0;1;2;…}. Vậy tập hợp E có vô số phần tử.
f. F = ∅ . Vậy tập hợp F không có phần tử nào.
g. G = {0;1;2;3}. Vậy tập hợp G có 4 phần tử
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
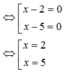
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
NV
11 tháng 9 2015
a/ x = 533
b/ x = 102
c/ 4x = 0 => x = 0
d/ 7x = 721 => x = 103
e/ x - 3 = 0 => x = 3
g/ x = 0
PN
11 tháng 9 2015
a,x:13=41
x=41x13
x=353
Vậy x=353 (tính lại nhé nếu mk tính sai)
b,1428:x=14
x=1428:4
x=102
Vậy x=102
c,4x:17=0
4x=0x17
4x=0
x=0:4
x=0
Vậy x = 0
d,7x-8=713
7x=713+8
7x=721
x=721:7
x=103
Vậy x = 103
e, 8(x-3)=0
x-3=0:8
x-3=0
x=0+3
x=3
Vậy x=3
g,0:x=0
Ta thấy 0 chia cho bất kỳ số tự nhiên nào khác 0 đều bằng 0.
=>x\(\in\)N*
Vậy x\(\in\)N*
Đề sai rồi bạn