Câu 39: Hình thang cân PQRS có độ dài đáy PQ = 20cm. Đáy RS ngắn hơn đáy PQ là 12cm. Độ dài cạnh bên PS bằng một nửa độ dài đáy PQ. Chu vi của hình thang PQRS là: A. 46cm B. 44cm C. 40cm D. 48cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2023
AB=CD-6=16-6=10(cm)
\(AD=\dfrac{AB}{2}=5\left(cm\right)\)
Vì ABCD là hình thang cân
nên \(AD=BC=5\left(cm\right)\)
Chu vi hình thang cân ABCD là:
\(AB+AD+CD+BC=5+5+10+16=36\left(cm\right)\)
Diện tích hình thang cân ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot AH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\cdot\left(10+16\right)=2\cdot26=52\left(cm^2\right)\)
KV
9 tháng 12 2023
Cạnh AB dài:
16 - 6 = 10 (cm)
Cạnh AD dài:
10 : 2 = 5 (cm)
Chu vi hình thang cân ABCD:
16 + 10 + 5 + 5 = 36 (cm)
Diện tích hình thang:
(16 + 10) × 4 : 2 = 52 (cm²)
CM
5 tháng 10 2017
Đáp án cần chọn là: C
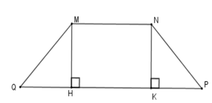
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 12 cm nên QH = KP = 40 − 12 2 = 14 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 12 + 40 ) .14 2 = 364 c m 2
14 tháng 11 2021
VÌ hình thang đó là hình thang cân
=> 2 cạnh bên bằng nhau
Tổng độ dài 2 cạnh bên là
46-28= 18(cm)
Mà 2 cạnh bên bằng nhau
=> Độ dài mỗi cạnh là 9 cm
VA
23 tháng 12 2021
VÌ hình thang đó là hình thang cân
=> 2 cạnh bên bằng nhau
Tổng độ dài 2 cạnh bên là
46-28= 18(cm)
Mà 2 cạnh bên bằng nhau
=> Độ dài mỗi cạnh là 9 cm
12 tháng 1 2023
PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)
Chọn B
Chọn B nhé