Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C B
Đề bài phải sửa thành "biết AD=AB" mới làm được
a/
ABCD là hình thàng cân => AD=BC
Mà AD=AB (gt)
=> AD=BC
b/
ABCD là hình thang cân
\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)
\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)
\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB=BC (cmt) => sđ cung AB = sđ cung BC (1)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)
\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)

a: Xét ΔAKD vuông tại K và ΔBHC vuông tại H có
AD=BC
góc D=góc C
=>ΔAKD=ΔBHC
=>CH=DK
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AB=HK
b: KH=AB=7cm
=>DK+HC=13-7=6cm
=>DK=HC=6/2=3cm
\(BH=\sqrt{13^2-3^2}=\sqrt{160}=4\sqrt{10}\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}\cdot BH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\sqrt{10}\left(7+13\right)=40\sqrt{10}\left(cm^2\right)\)

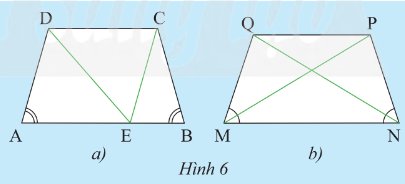
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)

D A B C H K 45
Kẻ 2 đường cao AH và BK
=> ABKH là hình chữ nhật
=> AB = HK = 13cm
=> DH = KC = (DC - HK) : 2 = (25 - 13) : 2 = 6cm
Trong tam giác AHD có : góc ADH = 450; góc AHD = 900 => góc DAH = 450
=> tam giác AHD vuông cân tại H
=> AH = DH = 6cm
Vậy SABCD = \(\frac{\left(AB+CD\right).AH}{2}=\frac{\left(13+25\right).6}{2}=114cm^2\)

Xét tam giác ABC và tam giác BKC có :
góc AHD = góc AKC = 90 độ ( gt )
AD = BC ( gt )
góc D = góc C ( gt )
=> tam giác ABC = tam giác BKC ( ch - gn )
=> DH = CK

`a)` Vì ABCD là hình thang cân
`=> AD = BC`
Có `AB = AD`
`=> BC = AB`
`b)`
Có `AB = AD`(GT)
`=>` tam giác `ABD ` cân
`=>` góc ADB = góc ABD 2
Vì `ABCD` là hình thang cân nên :
`AB//DC`
`=>` góc ABD = góc BDC 1
từ `(1); (2) =>` góc ADB = góc BDC
`=>` BD là pg cưa góc ADC
a: ABCD là hình thang cân
=>AD=BC
mà AD=AB
nên AB=BC
b: góc ABD=góc ADB
góc ABD=góc BDC
=>góc ADB=góc BDC
=>DB là phân giác của góc ADC