Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng các hệ thức lượng trong tam giác vuông ,ta được:
\(AH^2=BH.CH\)
\(AH.BC=AB.AC\)
Lớp 8 chưa học lượng giác mà??
a) Xét tam giác AHC vuông tại H và tam giác AHB vuông tại H
Áp dụng định lý Pytago cho cả 2 tam giác:
Tam giác AHC: AH^2= AC^2 - CH^2 (1)
TAM GIÁC AHB: AH^2 =AB^2 - BH^2 (2)
(1) (2) Suy ra 2AH^2 = AB^2 + AC^2 - CH^2 - BH^2
2AH^2 = BC^2 - CH^2 - BH^2
2AH^2 = (BH+CH)^2 - CH^2 - BH^2
2AH^2 = 2BH.CH
AH^2 = BH.CH
b) Xét tam giác AHB và tam giác CAB:
H^ = A^ = 90 độ
B^ chung
2 tam giác AHB và tam giác CAB đồng dạng trường hợp (g-g)
Suy ra AH/CA = HB/AB= AB/BC
Vậy AH.BC = AB.AC

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng với ΔABC
=>ΔHBA đồng dạng với ΔHAC
b: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
d: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

Xét △ACH vuông tại H và △BAH vuông tại H
Có: \(\widehat{CAH}=\widehat{HBA}\) (cùng phụ với \(\widehat{HAB}\))
=> △ACH ᔕ △BAH (g.g)
\(\Rightarrow\frac{AH}{BH}=\frac{CH}{AH}\)
=> AH . AH = BH . CH
=> AH2 = BH . CH
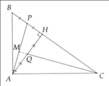
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh:△HBA=△ABC và góc BAH bằng góc BCA
b)Chứng minh AH2=BH.HC
c)Kẻ phân giác BD của góc ABC(D thuộc AC) cắt AH tại E. Cho AB = 15cm, AC = 20cm. Tính BC,AD, DC,BD
Gọi M là trung điểm ED.Kẻ EF vuông góc AB tại F.Chứng minh 3 đường thẳng EF,BH, AM đòng quy.