Cho tam giác ABC có M là trung điểm cạnh AB, N là trung điểm cạnh AC. Trên tia đối của tia NM lấy điểm P sao cho NP = MN. Chứng minh rằng:a) AMNCPN=b) CP = BM; CP ∥BM.c) MN ∥BC.d) Có nhận xét gìvểđộdài MN so với BC?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, C/m CP // AB
Xét ΔANM và ΔCNP. Ta có:
NM = NP (gt)
∠N1 = ∠N2 (đối đỉnh)
NA = NC (gt)
⇒ ΔANM = ΔCNP (c.g.c)
Nên: ∠A = ∠C1 (hai góc tương ứng)
Mà ∠A và ∠C1 ở vị trí so le trong
⇒ CP // AB
b, C/m MB = CP
Ta có: MA = CP (vì ΔANM = ΔCNP)
Mà MA = MB (gt)
⇒ MB = CP
c, C/m BC = 2MN
Nối BP. Xét ΔMBP và ΔCPB. Ta có:
BM = CP (gt)
∠B1 = ∠P1 (so le trong)
BP cạnh chung
⇒ ΔMBP = ΔCPB (c.g.c)
Nên: MP = BC (hai cạnh tương ứng)
Mà: MP = 2MN (vì N là trung điểm của MP)
⇒ BC = 2MN

a,Xét tg AMN và tg CPN có
\(\hept{\begin{cases}AN=NC\left(gt\right)\\NP=NM\left(gt\right)\\\widebat{ANM=\widebat{CNP\left(đ\right)}}\end{cases}}\)
\(\Rightarrow\)tg AMN = tg CPN ( c.g.g )
b, Vì tg AMN = tg CPN ( cma )
\(\hept{\begin{cases}\Rightarrow AM=CP\left(2\right)cạnhtứng\\MàAM=MB\left(gt\right)\end{cases}}\)
\(\Rightarrow\)CP=MP
c, Vì tg AMN = tg CPN ( cma )
\(\hept{\begin{cases}\Rightarrow\widebat{MAN=\widebat{PCN}\left(tu\right)}\\Mà2gócởSLT\end{cases}}\)
\(\Rightarrow\)CP//BM

a)
Xét tam giác AMN và tam giác CPN có:
AN=NC (N là trung điểm của AC)
\(\widehat{MNA}=\widehat{DNC}\)(2 góc đối đỉnh)
MN=NP
=> tam giác AMN= tam giác CPN(c-g-c)
b)Vì tam giác AMN= tam giác CPN
=>MA=PC ; \(\widehat{MAN}=\widehat{DCN}\)
Mà MA=MB(m là trung điểm của AB) ; Mà 2 góc này ở vị trí so le trong
=>CP=BM ;=>CP//BM
Vậy CP=BM và CP//BM
c)Xét tam giác MBC và tam giác PCM có:
MB=CP
\(\widehat{BMC}=\widehat{DCM}\)(MB//CP)
MC chung
=>tam giác MBC= tam giác CPM(c-g-c)
=>\(\widehat{PMC}=\widehat{BCM}\) ; MD=BC
Mà 2 goác này ở vị trí so le trong ; =>2MN=BC
=>MN//BC ; =>MN=\(\frac{1}{2}BC\)

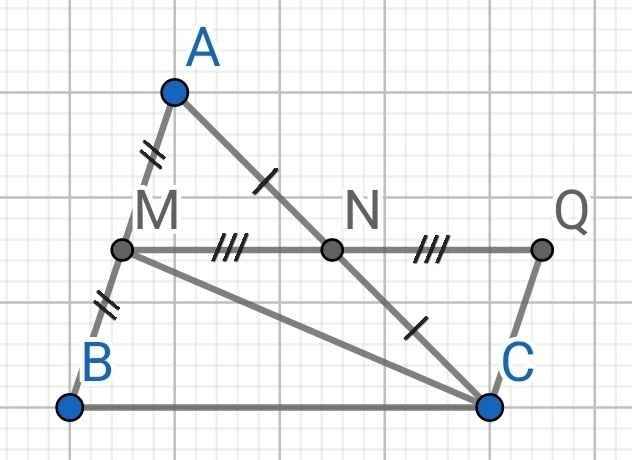
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC

a/ CM: tam giác NAM=tam giác NCP (c.g.c)
=>Góc MAN = Góc NCP
Mà 2 góc nằm ở vị trí so le trong
=>đpcm
b/Vì tam giác NAM= tam giác NCP(cmt)
=>AM=CP (1)
Mà AM=BM(gt) (2)
Từ (1) và (2) suy raBM=CP
c/ Nối B với P
CM Tam giác BMP= tam giác PCB(c.g.c)
=>BC=MP(cạnh tương ứng) (3)
Mà 2MN=MP (4)
Từ (3) và (4) suy ra đpcm
