Cho tam giác abc, điểm o nằm trong tam giác . Chứng minh OA+OC<BA+BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nguyễn Ngọc Sơn Lâm
Cho 5 số tự nhiên thỏa mãn
CMR: a=b=c=d=e
trần ngọc định
Cho E = . Chứng minh rằng : E <
giúp mình với mấy bạn ơi ?.........
giúp đi rồi mình kết bạn nha !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Đinh Đức Hùng
Cho A = 1 + 3 + 6 + 10 + .... + 4753 + 4851 + 4950
a ) Tính A
b ) CM Rằng : A không phải là số chính phương
Nguyễn Ngọc Hà
tính tổng:
a, A=Biết:
b, B=10.11+11.12+12.13+...+49.50
nguyen thi thanh thao
tinh A/B
A=1/2+1/3+...+1/2016
B=1/2015+2/2014+...+2014/2+2015/1
Bài toán 100
Cho tam giác ABC có trung tuyến AD. Trên AB lấy điểm M sao cho AM/AB = 1/4; Trên AC lấy điểm N sao cho AN/AC = 1/2. Đoạn MN cắt AD tại E. Hỏi tỉ s...

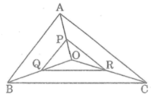
* Trong △ AOB ta có:
P trung điểm của OA (gt)
Q trung điếm của OB (gt)
Suy ra PQ là đường trung bình của △ AOB
Suy ra: PQ = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 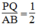 (1)
(1)
* Trong △ OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra PR là đường trung bình của tam giác OAC.
Suy ra: PR =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 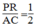 (2)
(2)
* Trong △ OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra QR là đường trung bình của tam giác OBC
Suy ra: QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 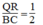 (3)
(3)
Từ (1), (2) và (3) suy ra: 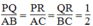
Vậy △ PQR đồng dạng △ ABC (c.c.c)


Vì OA=OB=OC
nên O là tâm đường tròn ngoại tiếp ΔABC
mà ΔABC đều
nên O là giao điểm của ba tia phân giác của các góc A,B,C

Xét ΔOAB có
M∈OA(gt)
N∈OB(gt)
\(\dfrac{OM}{OA}=\dfrac{ON}{OB}\left(=\dfrac{1}{3}\right)\)
Do đó: MN//AB(Định lí Ta lét đảo)
Xét ΔOAB có
M∈OA(gt)
N∈OB(gt)
MN//AB(cmt)
Do đó: \(\dfrac{MN}{AB}=\dfrac{OM}{OA}\)(Hệ quả của Định lí Ta lét)
⇔\(\dfrac{MN}{AB}=\dfrac{1}{3}\)(1)
Xét ΔAOC có
M∈OA(gt)
P∈OC(gt)
\(\dfrac{OM}{OA}=\dfrac{OP}{OC}\left(=\dfrac{1}{3}\right)\)
Do đó: MP//AC(Định lí Ta lét đảo)
Xét ΔOAC có
M∈OA(gt)
P∈OC(gt)
MP//AC(cmt)
Do đó: \(\dfrac{MP}{AC}=\dfrac{OM}{OA}\)(Hệ quả của Định lí ta lét)
hay \(\dfrac{MP}{AC}=\dfrac{1}{3}\)(2)
Xét ΔOBC có
N∈BO(gt)
P∈CO(gt)
\(\dfrac{ON}{OB}=\dfrac{OP}{OC}\left(=\dfrac{1}{3}\right)\)
Do đó: NP//BC(Định lí Ta lét đảo)
Xét ΔOBC có
N∈BO(gt)
P∈CO(gt)
NP//BC(cmt)
Do đó: \(\dfrac{NP}{BC}=\dfrac{ON}{OB}\)(Hệ quả của Định lí Ta lét)
⇔\(\dfrac{NP}{BC}=\dfrac{1}{3}\)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{MN}{AC}=\dfrac{MP}{AC}=\dfrac{NP}{BC}\)
Xét ΔMNP và ΔABC có
\(\dfrac{MN}{AC}=\dfrac{MP}{AC}=\dfrac{NP}{BC}\)(cmt)
Do đó: ΔMNP∼ΔABC(C-c-c)

Ta có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC < AB + BC + CA (vì OC < BC) Vậy ta có: OA + OB + OC < AB + BC + CA (1) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OC) + OB = AC + OB < AB + BC + CA (vì OB < AB) Vậy ta có: OA + OB + OC < AB + BC + CA (2) Từ (1) và (2), ta có: OA + OB + OC < AB + BC + CA Tương tự, ta có: OA + OB + OC = OA + OB + OC = (OB + OC) + OA = BC + OA > 0A + OB + OC (vì BC > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (3) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC > 0A + OB + OC (vì AB > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (4) Từ (3) và (4), ta có: OA + OB + OC > 0A + OB + OC Vậy ta có: 0A + OB + OC < AB + BC + CA < OA + OB + OC


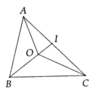
 tham khảo nha
tham khảo nha