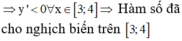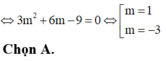Tìm giá trị lớn nhất của A= 2<m+p> +mp - m2 - p2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 1 2018
Đáp án A.
Điều kiện x ∈ ℝ
y = cos x + cos x − π 3 = cos x + cos x . cos π 3 + sin x . sin π 3 = cos x + 1 2 cos x + 3 2 sin x
= 3 2 cos x + 3 2 sin x
Cách 1: y = 3 3 2 cos x + 1 2 sin x = 3 sin x + π 3 Suy ra − 3 ≤ y ≤ 3
Vậy m = − 3 ; M = 3 và do đó M 2 + m 2 = 6
Cách 2:
Áp dụng bất đẳng thức Bunyakovsky ta có:
3 2 cos x + 3 2 sin x 2 ≤ 3 2 2 + 3 2 2 cos x 2 + sin x 2
⇔ 3 2 cos x + 3 2 sin x 2 ≤ 3 ⇔ − 3 ≤ y ≤ 3
⇒ M = 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = 3
Tương tự ta có m = − 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = − 3
⇒ M 2 + m 2 = 3 2 + − 3 2 = 6
Vậy ta chọn A.
31 tháng 5 2021
\(A=2\left(m+p\right)+mp-m^2-p^2\)
\(=\frac{4m+4m+2mp-2m^2-2p^2}{2}\)
\(=\frac{-\left(m-2\right)^2-\left(p-2\right)^2-\left(m-p\right)^2+8}{2}\le4\)
Đẳng thức xảy ra khi m=p=2
MM
1
29 tháng 4 2019
\(2A=4\left(m+p\right)+2mp-2m^2-2p^2=\left(-m^2+4m-4\right)+\left(-p^2+4p-4\right)+\left(-m^2+2mp-p^2\right)+8\)
\(=-\left(m-2\right)^2-\left(p-2\right)^2-\left(m-p\right)^2+8\le8\)
=> \(A\le4\)
"=" <=> m=p=2
