Tìm các số nguyên tố p sao cho các số sau cũng là số nguyên tố:
a}p+2 va p+10
b}p+10 va p+20
c}p+2;p+6;p+8;p+12;p+14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 8 2021
Câu b:
Đến đoạn này cũng xét như câu a
Câu c:
3 tháng 4 2018
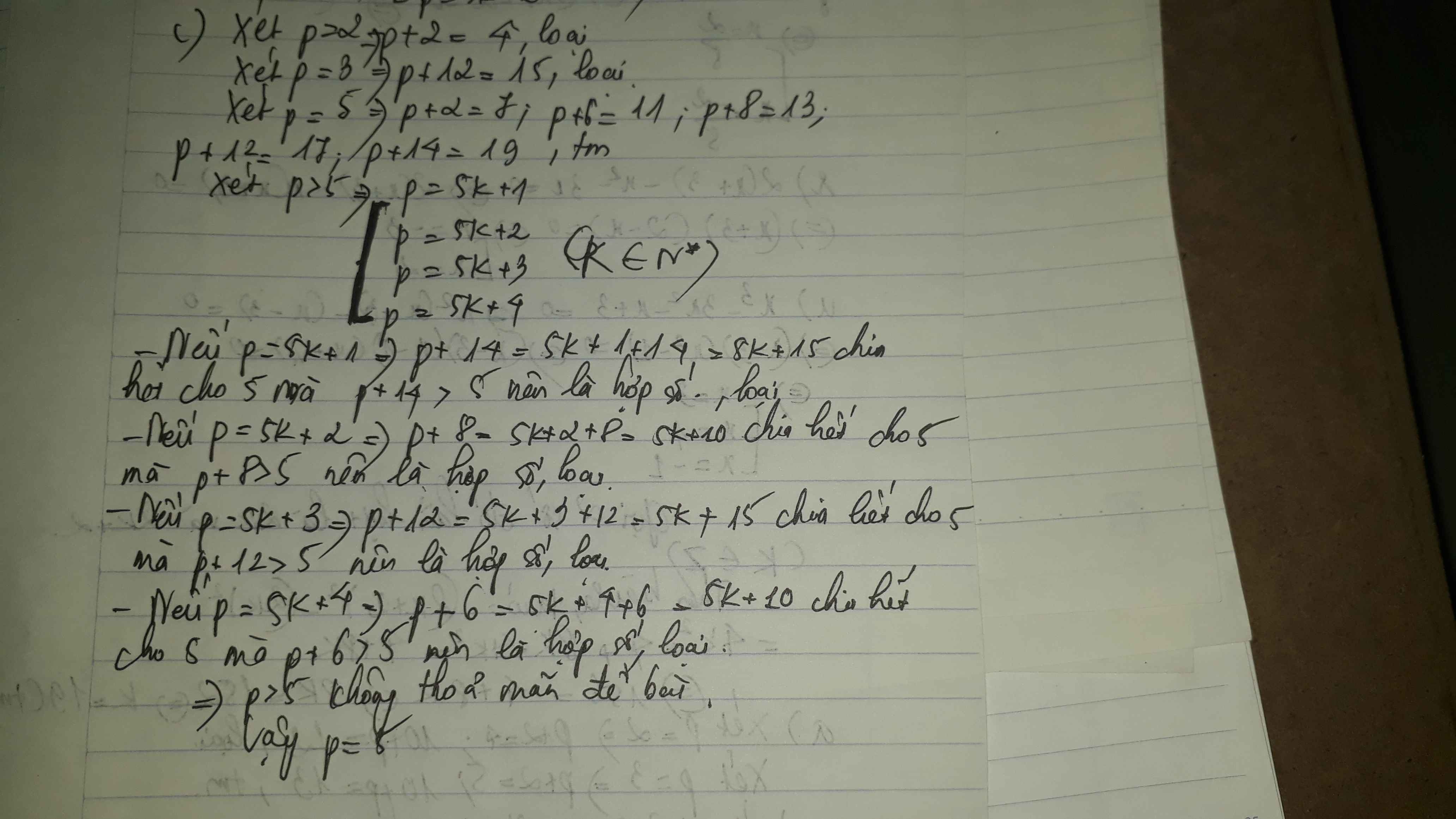
Vì pq +11 là số nguyên tố \(\Rightarrow\)pq +11 là số lẻ \(\Rightarrow\)pq là số chẵn \(\Rightarrow\)p \(⋮\)2 hoặc q\(⋮\)2
- p\(⋮\)2 mà q là số nguyên tố \(\Rightarrow\)q = 2
thay p = 2 vào 7p +q ta đc 14+ q mà 7p +q là số nguyên tố \(\Rightarrow\)14+q là số nguyên tố
\(\Rightarrow\)14+q ko chia hết cho 3 mà 14 chia 3 dư 2 \(\Rightarrow\)q \(⋮\)3 hoặc q chia 3 dư 2
- q chia 3 dư 2 \(\Rightarrow\)q có dạng 3k+2 (k là số tự nhiên)
thay q=3k+2;p=2 vào pq +11 ta đc
2(3k+2)+11=6k+4+11=6k+15=3(2k+5)\(⋮\)3 và 3(2k+5) > 3 (KTM vì pq +11 là số nguyên tố)
- q \(⋮\)3\(\Rightarrow\)q có dạng 3a(a là số tự nhiên)
mà q là số nguyên tố \(\Rightarrow\)q =1
2. chứng minh tương tự
đúng thì k nha
BG
1
AH
Akai Haruma
Giáo viên
2 tháng 12 2023
** Sửa đề: sao cho $p+2, p+10$ cũng là snt.
Lời giải:
Nếu $p$ chia hết cho $3$ thì do $p$ là snt nên $p=3$. Khi đó: $p+2=5; p+10=13$ cũng là snt (thỏa mãn)
Nếu $p$ chia $3$ dư $1$. Đặt $p=3k+1$ với $k$ tự nhiên.
Khi đó: $p+2=3k+3=3(k+1)\vdots 3$. Mà $p+2>3$ với mọi $p$ nguyên tố.
$\Rightarrow p+2$ không là snt theo yêu cầu đề (loại)
Nếu $p$ chia $3$ dư $2$. Đătk $p=3k+2$ với $k$ tự nhiên.
Khi đó: $p+10=3k+2+10=3k+12=3(k+4)\vdots 3$. Mà $p+10>3$ nên $p+10$ không là snt theo yêu cầu đề (loại)
Vậy $p=3$ là đáp án duy nhất.
NT
2
13 tháng 12 2016
Xét trường hợp p= 2=> p+10= 12﴾không phải là số nguyên tố﴿
Xét trường hợp p= 3=> p+ 10= 13; p+ 14= 17 ﴾đều là số nguyên tố﴿
Xét p>3=> p có một trong 2 dang 3k+1; 3k‐ 1
+﴿Với p= 3k+1=> p+14= 3k+1+14=3k+15 chia hết cho 3
+﴿Với p= 3k‐1=> p‐ 10= 3k‐ 1+ 10= 3k+9 chia hết cho 3
Vậy p= 3 thì p+10 và p+14 cũng là số nguyên tố
TK
0
26 tháng 7 2023
Bài 1 :
a) \(123456789+729=\text{123457518}⋮2\)
⇒ Số trên là hợp số
b)\(5.7.8.9.11-132=\text{27588}⋮2\)
⇒ Số trên là hợp số
Bài 2 :
a) \(P+2\&P+4\) ;à số nguyên tố
\(\Rightarrow\dfrac{P+2}{P+4}=\pm1\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{P+2}{P+4}=1\\\dfrac{P+2}{P+4}=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}P+2=P+4\\P+2=-P-4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}0.P=2\left(x\in\varnothing\right)\\2.P=-6\end{matrix}\right.\)
\(\Rightarrow P=-3\)
Câu b tương tự
26 tháng 7 2023
a,123456789+729=123457518(hợp số)
b,5x7x8x9x11-132=27588(hợp số)
Bài 2,
a,Nếu P=2=>p+2=4 và p+4=6 (loại)
Nếu P=3=>p+2=5 và p+4=7(t/m)
P>3 => P có dạng 3k+1 hoặc 3k+2(k ϵn,k>0)
Nếu p=3k+1=>p+2=3k+3 ⋮3( loại)
Nếu p=3k+2=>p+4=3k+6⋮3(loại)
Vậy p=3 thỏa mãn đề bài
b,Nếu p=2=>p+10=12 và p+14=16(loại)
Nếu p=3=>p+10=13 và p+14=17(t/m)
Nếu p >3=>p có dạng 3k+1 hoặc 3k+2
Nếu p=3k+1=>p+14=3k+15⋮3(loại)
Nếu p=3k+2=>p+10=3k+12⋮3(loại)
Vậy p=3 thỏa mãn đề bài.
a, + Nếu p = 3k mà p là số nguyên tố
=> p = 3
=> p + 2 = 5
và p + 10 = 13 (đều là số nguyên tố, chọn)
+ Nếu p = 3k + 1
=> p + 2 = 3k + 3 chia hết cho 3, là hợp số (loại)
+ Nếu p = 3k + 2
=> p + 10 = 3k + 12 chia hết cho 3, là hợp số (loại)
Vậy p = 3
b, Xét 3 trường hợp p = 3k; p = 3k + 1; p = 3k + 2
c, Xét 5 trường hợp 5k; 5k + 1; 5k + 2; 5k + 3; 5k + 4
dễ mà bạn
thử chọn đi . ko nhìu đâu