Giải phương trình lượng giác biến đổi về dạng \(a.sin+b.cosx=c\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9D
1
3 tháng 10 2021
\(sinx=\dfrac{2tan\dfrac{x}{2}}{tan^2\dfrac{x}{2}+1}\)
\(cosx=\dfrac{1-tan^2\dfrac{x}{2}}{1+tan^2\dfrac{x}{2}}\)
Đặt \(t=tan\dfrac{x}{2}\)
Khi đó pt: \(\Rightarrow a\cdot\dfrac{2t}{t^2+1}+b\cdot\dfrac{1-t^2}{1+t^2}=c\)
\(\Rightarrow2t\cdot a+\left(1-t^2\right)\cdot b=\left(1+t^2\right)\cdot c\)
7 tháng 3 2022
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
CM
4 tháng 11 2018
Đáp án B
Ta có : 2 x 3 + 2 x 2 - 3 x + 10 = 2 x 3 + x 2 – 10
⇔ 2 x 3 + 2 x 2 - 3 x + 10 - 2 x 3 - x 2 + 10 = 0
⇔ x 2 – 3 x + 20 = 0
Phương trình trên là phương trình bậc hai một ẩn với a = 1; b = -3 và c = 20.
DK
6 tháng 12 2018
Đáp án : D
Các kết luần đúng: 1,4,5
Đột biến cấu trúc NST có các dạng : mất đoạn , lặp đoạn, đảo đoạn, chuyển đoạn
Đột biến NST thường ảnh hưởng rất nghiêm trọng đến sức sống sinh vật, nhưng không phải đột biến nào cũng thế. Một ví dụ điển hình là sự trao đổi chéo cân của các NST trong kì đầu giảm phân 1, làm tăng khả năng xuất hiện biến dị tổ hợp có vai trò quan trọng với tiến hóa
Các đột biến cấu trục NST là nguyên liệu cho quá trình tiến hóa của sinh vật.
Đột biến nào di truyền được cũng là nguyên liệu cho tiến hóa chọn lọc. Vd. Đột biến chuyển đoạn roberson
HH
1
PT
1
CM
9 tháng 10 2017
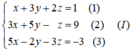
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3), phương trình (2) giữ nguyên ta được:
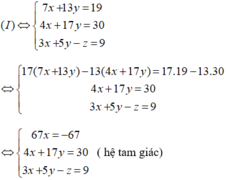
Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.
Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)
\(asinx+bcosx=c\)
\(\Leftrightarrow\frac{a}{\sqrt{a^2+b^2}}sinx+\frac{b}{\sqrt{a^2+b^2}}cosx=\frac{c}{\sqrt{a^2+b^2}}\)(1)
Có \(\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2=1\)nên ta đặt \(\frac{a}{\sqrt{a^2+b^2}}=siny,\frac{b}{\sqrt{a^2+b^2}}=cosy\)
Phương trình (1) tương đương với:
\(sinxsiny+cosxcosy=\frac{c}{\sqrt{a^2+b^2}}\)
\(\Leftrightarrow cos\left(x-y\right)=\frac{c}{\sqrt{a^2+b^2}}\)
Nếu \(\left|\frac{c}{\sqrt{a^2+b^2}}\right|\le1\Leftrightarrow a^2+b^2\ge c^2\)phương trình có nghiệm.
Nếu \(\left|\frac{c}{\sqrt{a^2+b^2}}\right|>1\Leftrightarrow a^2+b^2< c^2\)phương trình vô nghiệm.
Em cảm ơn thầy rất nhiều ạ