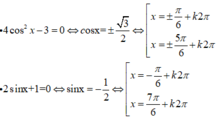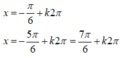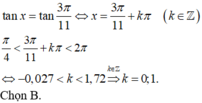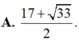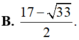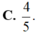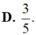Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương trình ⇔ 1 2 sin 2 x + 3 2 cos 2 x = 3 2 ⇔ sin 2 x + π 3 = 3 2
⇔ sin 2 x + π 3 = sin π 3 ⇔ 2 x + π 3 = π 3 + k 2 π 2 x + π 3 = π − π 3 + k 2 π ⇔ x = k π x = π 6 + k π , k ∈ ℤ .
= 0 < k π < π 2 ⇔ 0 < k < 1 2 → k ∈ ℤ không có giá trị k thỏa mãn.
= 0 < π 6 + k π < π 2 ⇔ − 1 6 < k < 1 3 → k ∈ ℤ k = 0 → x = π 6 .
Chọn đáp án A.
Đáp án B.
Điều kiện x > 1 + 33 2
Đặt t = log3x <=> x = 3t
Ta có bất phương trình: 9t < 4.4t + 3t + 8
⇔ 4 . 4 9 t + 1 3 t + 8 1 9 t > 1
Hàm số f ( t ) = 4 . 4 9 t + 1 3 t + 8 1 9 t nghịch biến và f(2) = 1 nên ta có t < 2 tìm được tập nghiệm là 1 + 33 2 ; 9 có độ dài trên trục số là 9 - 1 + 33 2 = 17 - 33 2 .
Đáp án B
Phương pháp:
Sử dụng các công thức giải phương trình lượng giác cơ bản:
Chọn B
Sử dụng các công thức giải phương trình lượng giác cơ bản:
