Gieo một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần xuất hiện mặt sấp là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 12 2017
Đáp án C
Gọi A k là biến cố lần thứ k xuất hiện mặt sấp
ta có P ( A k ) = 1 2 và
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
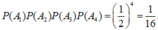
a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
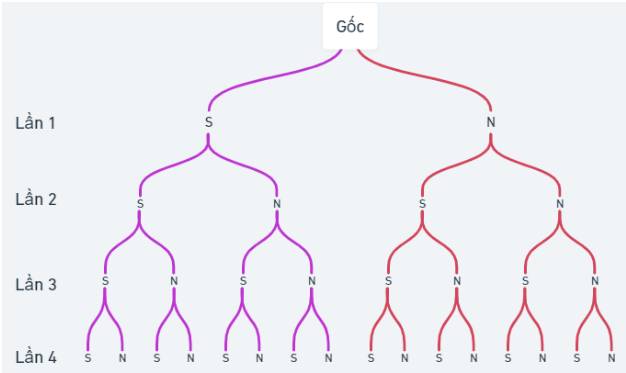
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).
HK
29 tháng 11 2017
xác suất mặt ngửa của đồng A là 1/2,của đồng B là 1/4
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 12 2020
Không gian mẫu: \(\left\{SS;NN;SN;NS\right\}\)
Xác suất: \(P=\dfrac{2}{4}=\dfrac{1}{2}\)
TT
19 tháng 4 2023
sao 2/4 được ạ. xuất hiện mặt sấp đúng 1 lần chứ có phải là đúng lần 1 đâu mà biến cố là 2
CM
25 tháng 11 2019
Vì A i là biến cố: "Mặt sấp xuất hiện ở lần gieo thứ i" nên A i ¯ là biến cố: "Mặt ngửa xuất hiện ở lần gieo thứ ". Do đó A 1 ¯ ∪ A 2 ¯ ∪ A 3 ¯ là biến cố: "Mặt ngửa xuất hiện ít nhất một lần". Chọn C.
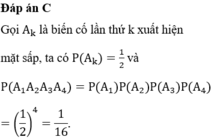
Tham khảo:
Số trường hợp xảy ra có thể là: 24 = 16
Chỉ có duy nhất một trường hợp cả 4 lần đều xuất hiện sấp.
Xác suất cần tính là: P(X) = 1/16
Chọn đáp án C.
Gọi A là biến cố "Cả 4 lần đều là mặt sấp".
\(\Rightarrow\left|\Omega\right|=2^4\)
\(\left|\Omega_A\right|=1\)
\(\Rightarrow P\left(A\right)=\dfrac{1}{2^4}=\dfrac{1}{16}\)