Hình chữ nhật ABCD có AC cắt DB tại O biết AB=6cm,BC=8cm độ dài OA là mn chỉ cần ghi cách giải thui ạ hoqq cần vẽ hình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2023
a: DB=căn 8^2+6^2=10cm
HD=AD^2/BD=3,6cm
HB=10-3,6=6,4cm
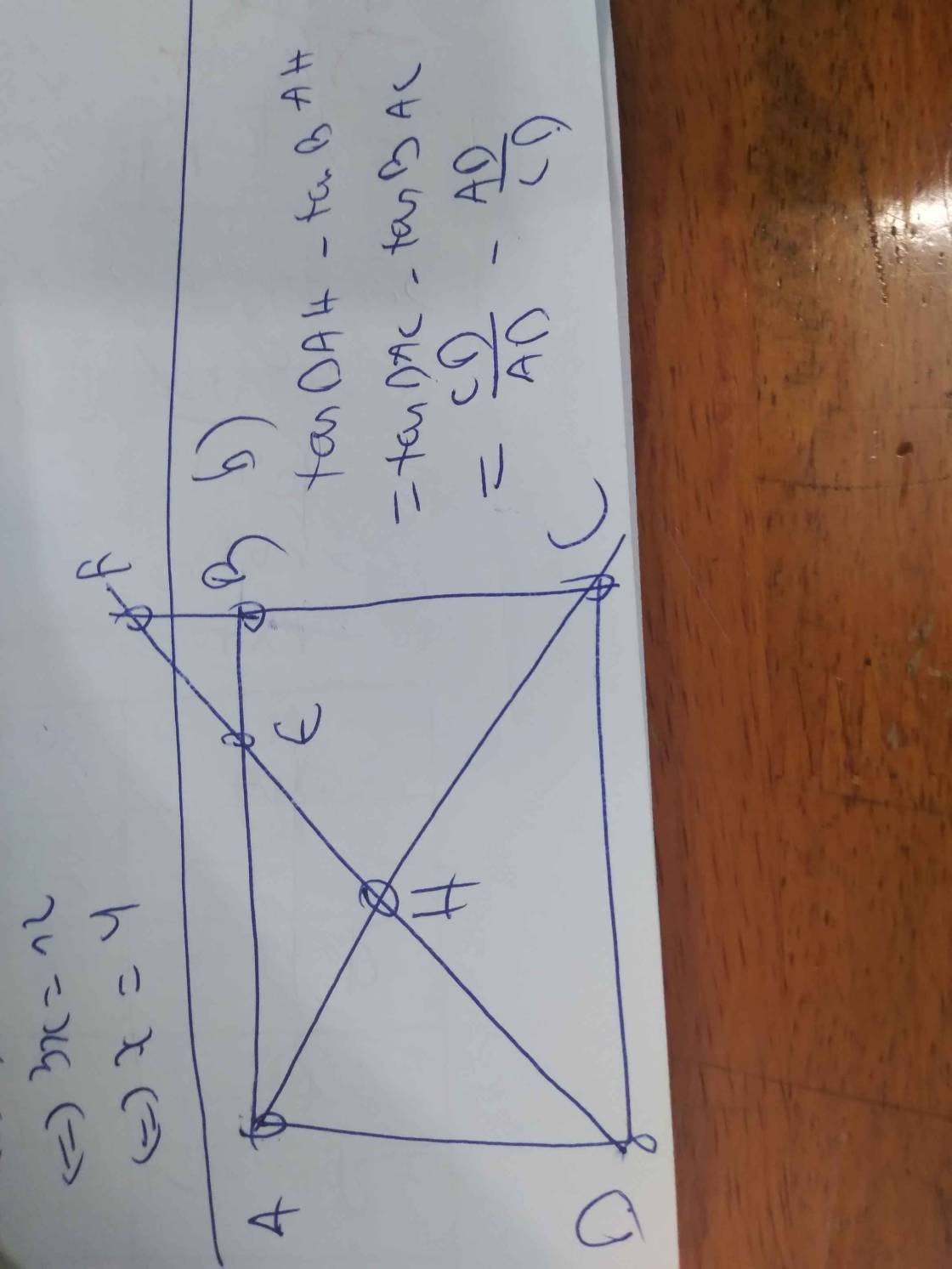
b:
AH=6*8/10=4,8cm
AM=AB^2/AH=8^2/4,8=40/3(cm)
14 tháng 3 2022
Bài 2:
a: BC=10cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>BH=36/10=3,6(cm)
=>CH=6,4(cm)
12 tháng 3 2023
a: góc AEH=1/2*180=90 độ
=>HE vuông góc AB
góc AFH=1/2*180=90 độ
=>HF vuông góc AC
Vì góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: AEHF làhình chữ nhật
=>góc AFE=góc AHE=góc B
=>góc B+góc FCB=180 độ
=>BEFC nội tiếp
22 tháng 7 2021
Xét ΔADC vuông tại D có DE là đường cao ứng với cạnh huyền AC nên ta có:
\(\dfrac{1}{DE^2}=\dfrac{1}{AD^2}+\dfrac{1}{DC^2}\)
\(\Leftrightarrow\dfrac{1}{DE^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{25}{576}\)
\(\Leftrightarrow DE^2=23.04\)
hay DE=4,8(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAFD vuông tại A có AE là đường cao ứng với cạnh huyền DF, ta được:
\(DA^2=DE\cdot DF\)
\(\Leftrightarrow DF=\dfrac{6^2}{4.8}=7,5\left(cm\right)\)
Ta có: DE+EF=DF(E nằm giữa D và F)
nên EF=DF-DE=7,5-4,8=2,7(cm)
Áp dụng định lí Pytago vào ΔADE vuông tại E, ta được:
\(AD^2=AE^2+DE^2\)
\(\Leftrightarrow AE^2=6^2-4.8^2=12.96\)
hay AE=3,6(cm)
Xét ΔAEF vuông tại E và ΔABC vuông tại B có
\(\widehat{BAC}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(g-g)
Suy ra: \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AF=\dfrac{AE\cdot AC}{AB}=\dfrac{3.6\cdot8}{6}=4.8\left(cm\right)\)
Ta có: AF+FB=AB(F nằm giữa A và B)
nên BF=AB-AF=8-4,8=3,2(cm)