Câu 7. Một viên bi được ném theo phương ngang với vận tốc 4 m/s từ độ cao h= 3m so với mặt đất.Tầm ném xa của viên bi gần bằng giá trị nào sau đây? Cho g = 10 m/s2
A. 2,2 m B. 1,41 m C.2,82 m D. 3,1 m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v_0=20mm/s=0,02m/s\)
a)Đây là bài toán vật rơi tự do.
Phương trình quỹ đạo: \(y=\dfrac{g}{2v_0}x^2=\dfrac{10}{2\cdot0,02}x^2=250x^2\)
Phương trình vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{100t^2+4\cdot10^{-3}}\left(m/s\right)\)
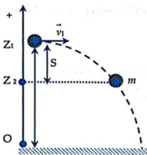
b)Thời gian viên bi đạt độ cao cực đại:
\(v=v_0-gt\Rightarrow t=\dfrac{v-v_0}{-g}=\dfrac{0-0,02}{-10}=0,002s\)
Độ cao vật đạt cực đại:
\(H=h_0+\dfrac{v_0^2}{2g}=25+\dfrac{0,02^2}{2\cdot10}=25,00002m\)
c)Thời gian vật quay lại vị trí ban đầu sẽ bằng 2 lần thời gian vật đi đến độ cao cực đại.
\(\Rightarrow T=2t=0,004s\)
d)Thời gian viên đá rơi từ độ cao cực đại đến khi chạm đất là:
\(t'=\sqrt{\dfrac{2h_{max}}{g}}=\sqrt{\dfrac{2\cdot25,00002}{10}}\approx2,236s\)
Thời gian để bi chạm đất: \(T'=t+t'=2,238s\)
Vận tốc bi trước khi chạm đất:
\(v=\sqrt{v_0^2+\left(gt\right)^2}=\sqrt{0,02^2+\left(10\cdot2,238\right)^2}=22,38m/s\)

Phương trình chuyển động ném xiên của viên bi:
Theo trục Ox: \(x=\left(v_0\cos\alpha\right)t\)
Theo trục Oy: \(y=\left(v_0\sin\alpha\right)t-\dfrac{1}{2}gt^2\)
Phương trình quỹ đạo của viên bi: \(y=\dfrac{-g}{2v_0^2\cos^2\alpha}x^2+\left(\tan\alpha\right)x\)
Để tầm xa trên mặt bàn cực đại thì viên bi phải bay sát mép bàn và hợp với phương ngang 1 góc 45 độ
Dễ chứng minh: \(\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\)
Chứng minh: Ta có: \(v_x=v_y\Leftrightarrow v^2x=v^2y\) (1)
\(v^2x=v_0^2\cos^2\alpha\left(2\right)\) và \(v^2y-v_0^2\sin^2\alpha=-2gh\Rightarrow v^2y=-2gh+v_0^2\sin^2\alpha\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow v_0^2\cos^2\alpha=v_0^2\sin^2\alpha-2gh\Rightarrow\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\) ( Done :D )
Tại mặt bàn: \(y=h\Leftrightarrow-\dfrac{g}{2v_0^2\cos^2\alpha}x^2+\left(\tan\alpha\right)x=h\left(4\right)\)
(4) có 2 nghiệm x1 < x2
Gọi x1 là khoảng cách từ chỗ ném viên bi đến chân bàn H
x2 là tầm xa cực đại trên mặt bàn của viên bi
\(\left(4\right)\Leftrightarrow x=\dfrac{v_0^2}{g}\left(\sin\alpha\cos\alpha\pm\dfrac{\cos\alpha\sqrt{v_0^2\sin^2\alpha-2gh}}{v_0}\right)\)
Ta đã chứng minh được: \(\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\) \(\Rightarrow\sin\alpha=\sqrt{\dfrac{1}{2}+\dfrac{gh}{v_0^2}}\)
\(\Rightarrow x_1=\dfrac{v_0^2}{g}\left[-\dfrac{1}{2}+\dfrac{gh}{v_0^2}+\sqrt{\dfrac{1}{4}-\left(\dfrac{gh}{v_0^2}\right)^2}\right]\)
\(\Rightarrow x_2=\dfrac{v_0^2}{g}\left[\dfrac{1}{2}-\dfrac{gh}{v_0^2}+\sqrt{\dfrac{1}{4}\left(\dfrac{gh}{v_0^2}\right)^2}\right]\)
Vậy......

Đáp án C.
Tốc độ khi chạm đất của vật rơi tự do: v = 2 g h
Tốc độ khi chạm đất của vật bị ném ngang:
v ' = v 0 2 + 2 g h > v

Chọn C.
Tốc độ khi chạm đất của vật rơi tự do: v= 2 g h
Tốc độ khi chạm đất của vật bị ném ngang:
![]()


Do vật rơi tự do tức là vật chỉ chịu tác dụng của trọng lực, thì cơ năng của vật là một đại lượng bảo toàn tức là

<=> t = 0,8s
\(L=v\cdot\sqrt{\dfrac{2h}{g}}=4\cdot\sqrt{\dfrac{2\cdot3}{10}}=3,1\left(m\right)\)
Chọn D