mng giúp mk câu 35 vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TN
0

MN
1
PT
1

7 tháng 11 2021
a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)
QN
0


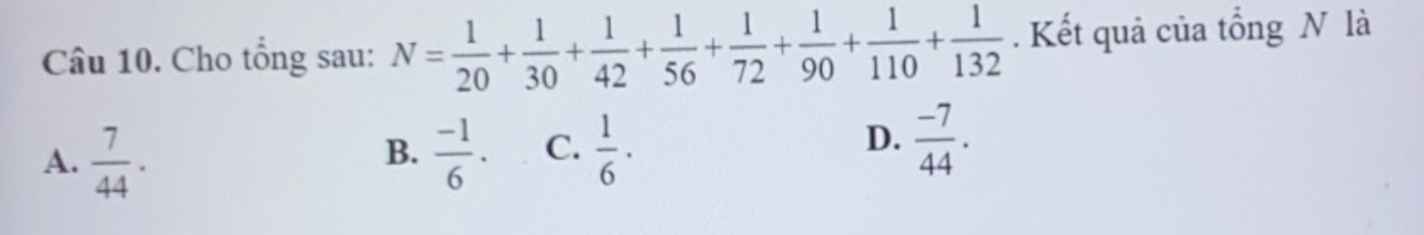
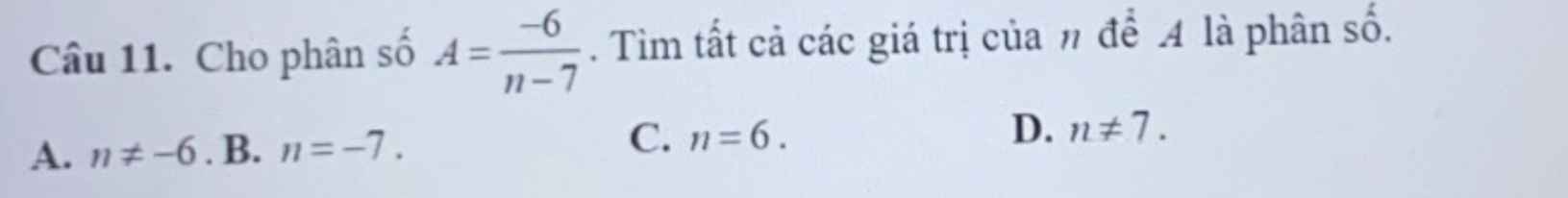
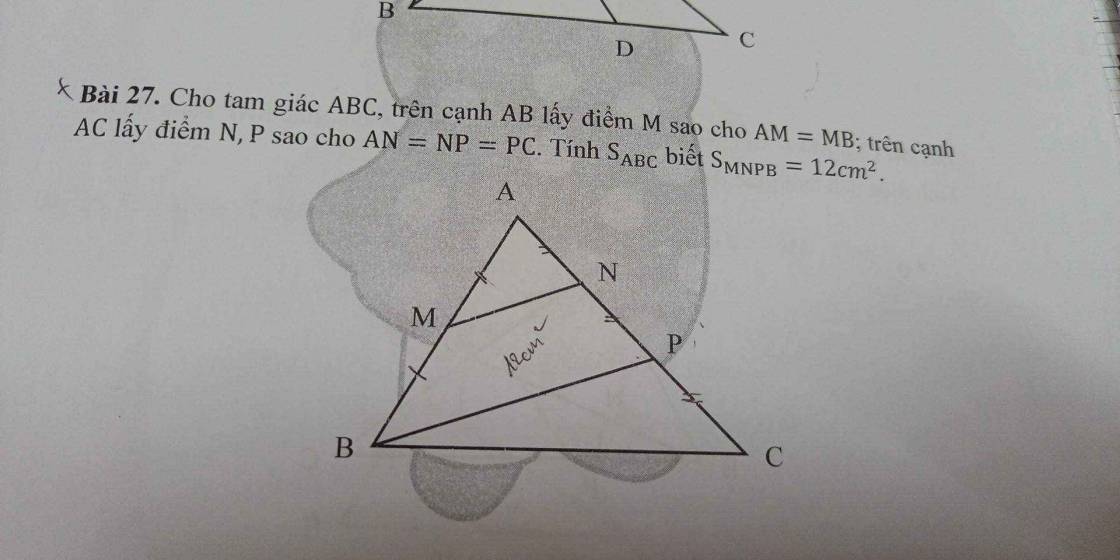






Lời giải:
\(\lim\limits_{x\to 2}\frac{x^2+ax+b}{2x^2-x-6}=\lim\limits_{x\to 2}\frac{x^2+ax+b}{(x-2)(2x+3)}\)
Để giới hạn này là hữu hạn thì $x^2+ax+b\vdots x-2$
$\Rightarrow 2^2+a.2+b=0\Leftrightarrow 2a+b=-4$
Đáp án A.
\(2x^2-x-6=0\) có 1 nghiệm \(x=2\)
Do đó giới hạn đã cho là hữu hạn khi và chỉ khi \(x^2+ax+b=0\) cũng có 1 nghiệm \(x=2\)
\(\Rightarrow4+2a+b=0\Rightarrow b=-2a-4\)
Vậy:
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax-2a-4}{2x^2-x-6}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)+a\left(x-2\right)}{\left(x-2\right)\left(2x+3\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+a+2\right)}{\left(x-2\right)\left(2x+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+a+2}{2x+3}=\dfrac{a+4}{7}\)
\(\Rightarrow\dfrac{a+4}{7}=\dfrac{3}{2}\Rightarrow a=\dfrac{13}{2}\Rightarrow b=-2a-4=-17\)
\(\Rightarrow2a+b=-4\)