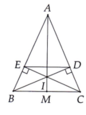
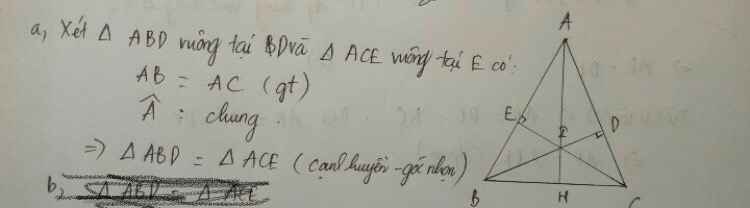Cho ΔABCnhọn có AB=AC. Kẻ BD ⊥AC tại D, kẻ CE⊥AB tại E, I là giao điểm của BD và CE.Chứng minh \(AI\perp...
Đọc tiếp
Cho ΔABCnhọn có AB=AC. Kẻ BD ⊥AC tại D, kẻ CE⊥AB tại E, I là giao điểm của BD và CE.Chứng minh \(AI\perp BC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2023
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
=>BE=DC
=>AE=AD
b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
=>ΔAEI=ΔADI
=>góc EAI=góc DAI
=>AI là phân giác của góc BAC
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
=>A,I,M thẳng hàng
15 tháng 5 2023
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `2\Delta` vuông và `BEC` và `CDB`:
`\text {BC chung}`
$\widehat {B} = \widehat {C}$
`=> \Delta BEC = \Delta CDB (ch-gn)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AE + BE}\\\text{AC = AD + CD}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BE = CD}\end{matrix}\right.\)
`-> \text {AE = AD}`
Xét `2\Delta` vuông `AEI` và ` ADI`:
`\text {AE = AD}`
`\text {AI chung}`
`=> \Delta AEI = \Delta ADI (ch-cgv)`
`->` $\widehat {EAI} = \widehat {DAI} (\text {2 góc tương ứng})$
`-> \text {AI là tia phân giác của}` $\widehat {EAD}$
Mà \(\text{E}\in\text{AB, D}\in\text{AC}\)
`-> \text {AI là tia phân giác của}` $\widehat {BAC}$ `(1)`
`c,`
Vì M là trung điểm của AC
`-> \text {AM là đường trung tuyến của} \Delta ABC` `(2)`
Từ `(1)` và `(2)`
`-> \text {Ba điểm A, I, M thẳng hàng.}`
16 tháng 11 2023
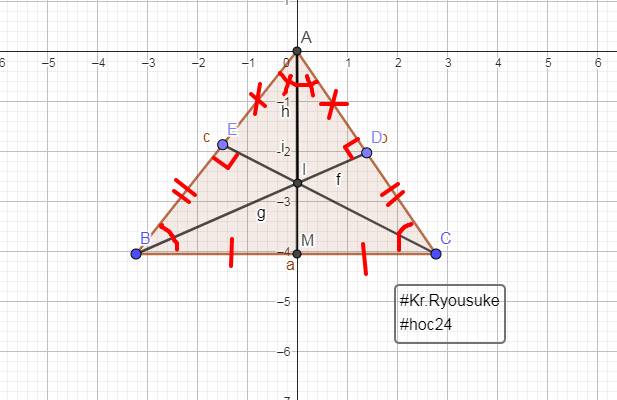
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
=>EI=DI
c: ΔABD=ΔACE
=>BD=CE
BI+DI=BD
CI+EI=CE
mà EI=DI và BD=CE
nên BI=CI
IB=IC
AB=AC
Do đó: AI là đường trung trực của BC
=>AI\(\perp\)BC
15 tháng 12 2020
bạn không được nói vậy , nói thế là khinh người khác và đây là nơi chúng ta giao lưu giúp nhau mà , nên bạn không được nói bậy như thế.
C
6 tháng 2 2018
ta có AD+DC=AC
=>7+1=A
=>AC=8 CM
mà AB=AC( TAM GIÁC ABC CÂN TẠI A)
MẶT KHÁC AC=8 cm=>AB=8CM
ap dụng định lý py-ta-go cho tam giác ADB vuông tại D
=>AD^2+BD^2=AB^2
=>7^2+BD^2=8^2
=>BD^15
=> BD= CĂN 15(BD>0)
ÁP DỤNG ĐỊNH LÝ PY TA GO CHO TAM GIÁC BDC VUÔNG TẠI D
BD^2+DC^2+BC^2
=>CĂN 15^2+1^2=BC^2
=>15+1=BC^2
=>16=BC^2
=>BC=4(BC>0)
=>
C
6 tháng 2 2018
a) xét tam giác AEC và tam giác ADB
góc ADB=góc AEC(=90 độ)
AB=AC ( Tam giác abc cân tại A)
góc A chung
Do đó tam giác AEC= tam giác ADB
b) Xét tam giác AEI và tam giác ADI có
góc AEI=ADI(=90 độ)
AD=AE(câu a)
AI chung
Do đó tam giác AEI = tam giác ADI
=> góc EAI=DAI (hai góc tương ứng)(1)
mà AI nằm giữa hai tia AB và AC(2)
Từ (1) và(2) AI là phân giác của hóc A
24 tháng 2 2022
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
Suy ra: BE=CD
b: Ta có: ΔEBC=ΔDCB
nên \(\widehat{ECB}=\widehat{DBC}\)
hay ΔIBC cân tại I
Ta có: AE+EB=AB
AD+DC=AC
mà AB=AC
và EB=DC
nên AE=AD
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại I
Do đó: I là trực tâm của ΔABC
Suy ra: AI\(\perp\)BC
mà AK\(\perp\)BC
nên A,I,K thẳng hàng
=>AK,BD,CE đồng quy
