Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)

vuông tại A, D chứ vuông tại đâu. học toán rùi mà ko biết là sao ?

Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
Giải:
Xem hình vẽ
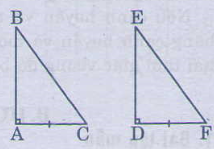
* Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)

Bổ sung thêm một điều kiện :
Ta có :
1) AB=ED
=> ΔABC=ΔDEF (2 cạnh góc vuông)
2)BCAˆ=EFDˆ
=> ΔABC=ΔDEF(g.c.g)
Bổ sung thêm một điều kiện :
Ta có :
1) AB=ED
=> ΔABC=ΔDEF (2 cạnh góc vuông)
2)BCAˆ=EFDˆ
=> ΔABC=ΔDEF(g.c.g)

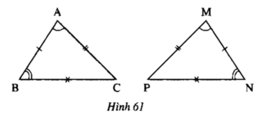
Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
kí hiệu: ΔABC = ΔMNP

Vì nếu 3 góc bằng nhau thì cả 2 tam giác đều sẽ là tam giác đều nên ko cần phải chứng minh 2 tam giác bằng nhau nữa
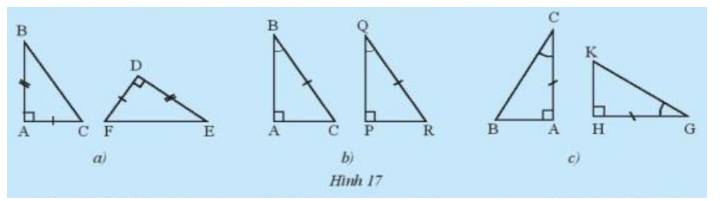
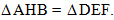
Các trường hợp bằng nhau của tam giác vuông:
-Hai cạnh góc vuông
-Cạnh góc vuông-góc nhọn kề
-Cạnh huyền-góc nhọn
-Cạnh huyền-cạnh góc vuông