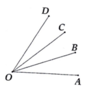
Cho góc AOD có số đo bằng 120 . Vẽ các tia OB, OC cùng thuộc một nửa mặt phẳng bờ chứa tia OA và tia OD sao cho các góc AOB, BOC, COD bằng nhau. Tìm tia phân giác của các góc trong hình vẽ.Kết quả
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2020
Bài làm
a) Vì \(\widehat{AOB}=\widehat{BOC}\)( gt )
=> OB là tia phân giác của góc AOC.
Vì \(\widehat{BOC}=\widehat{COD}\)( gt )
=> OC là tia phân giác của góc BOD.
b) Nếu OM là tia phân giác của góc AOD
Thì: \(\widehat{DOM}=\widehat{MOA}\)
Mà \(\widehat{DOM}+\widehat{MOA}=120^0\)
=> \(\widehat{DOM}=\widehat{MOA}=\frac{120^0}{2}=60^0\)
Ta có: \(\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\frac{120^0}{3}=40^0\)
Lại có: \(\widehat{AOB}+\widehat{BOM}=\widehat{MOA}\)
Hay \(40^0+\widehat{BOM}=60^0\)
\(\Rightarrow\widehat{BOM}=60^0-40^0=20^0\) (3)
Mặt khác: \(\widehat{COD}+\widehat{MOC}=\widehat{MOD}\)
hay \(40^0+\widehat{MOC}=60^0\)
\(\Rightarrow\widehat{MOC}=60^0-40^0=20^0\) (4)
Từ (3) và (4), ta được: \(\widehat{BOM}=\widehat{MOC}\left(=20^0\right)\)
=> OM là tia phân giác của góc BOC.
Vậy nếu OM là tia phân giác của góc AOD thì OM có là tia phân giác của góc BOC.
# Học tốt #
10 tháng 4 2019
Theo bài ra ta có hình vẽ:
a, Vì OB nằm giữa OA và OC \(\Rightarrow\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\Rightarrow45^o+\widehat{BOC}=120^o\)
\(\Rightarrow\widehat{BOC}=120^o-45^o=75^o\)
b, Vì OD là tia đối tia OC \(\Rightarrow\widehat{COD}=180^o\)
Vì OA nằm giữa OC và OD \(\Rightarrow\widehat{AOC}+\widehat{AOD}=\widehat{COD}\Rightarrow120^o+\widehat{AOD}=180^o\)
\(\Rightarrow\widehat{AOD}=180^o-120^o=60^o\)
c, Vì OK là tia phân giác của \(\widehat{AOD}\Rightarrow\widehat{AOK}=\widehat{DOK}=\frac{\widehat{AOD}}{2}\)
\(\Rightarrow\widehat{AOK}=\widehat{DOK}=\frac{60^o}{2}=30^o\)
Vì OA nằm giữa OB và OK \(\Rightarrow\widehat{AOB}+\widehat{AOK}=\widehat{BOK}\Rightarrow45^o+30^o=\widehat{BOK}\)
\(\Rightarrow\widehat{BOK}=75^o\)
Vì OB nằm giữa OK và OC và \(\widehat{BOK}=\widehat{BOC}\) => OB là tia phân giác của \(\widehat{COK}\)
10 tháng 4 2019
BÀI GIẢI
trên cùng nửa mặt phẳng bờ chứa tia OA,AOB<AOC
=> Tia OB là tia nằm giữa
Vì OB là tia nằm giữa nên ta có:
AOB + BOC = AOC
Thay AOB=45 độ; AOC=120 độ,ta có:
45 độ +BOC= 120 độ
BOC=75 độ
VN
15 tháng 3 2017
(Bạn tự vẽ hình!)
- Tia phân giác đầu tiên là \(Ob\)
Giải thích: Ta có: \(\widehat{cOb}+\widehat{bOa}=\widehat{cOa}\)
\(\Rightarrow\widehat{cOb}=\widehat{cOa}-\widehat{bOa}=80-40=40\)độ
Vậy: \(\widehat{cOb}=\widehat{bOa}=\frac{\widehat{cOa}}{2}\)
Mà \(Ob\)nằm giữa \(Oc;Oa\Rightarrow..\)
- Tia phân giác thứ 2 là \(Oc\)
Giải thích: Ta có: \(\widehat{dOb}+\widehat{bOa}=\widehat{dOa}\)
\(\Rightarrow\widehat{dOb}=\widehat{dOa}-\widehat{bOa}=120-40=80\)độ
\(\widehat{dOc}+\widehat{cOb}=\widehat{dOb}\)
\(\Rightarrow\widehat{dOc}=\widehat{dOb}-\widehat{cOb}=80-40=40\)độ
Vậy: \(\widehat{dOc}=\widehat{cOb}=\frac{\widehat{dOb}}{2}\)
Mà \(Oc\)nằm giữa \(Od;Ob\Rightarrow..\)
CM
30 tháng 4 2017
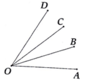
a) Ta có A O B ^ < A O C ^ nên tia OB nằm giữa hai tia OA và OC. Theo tính chất cộng góc, suy ra 20°, nên A O B ^ = B O C ^ . Vậy OB là tia phân giác của góc AOC.
b) Tương tự ý a), tính được
C O D ^ = 20° và B O D ^ = 40°.
c) Ta có B O C ^ = C O D ^ = B O D ^ 2 (cùng bằng 20°). Do đó, tia OC là tia phân giác của góc BOD.
