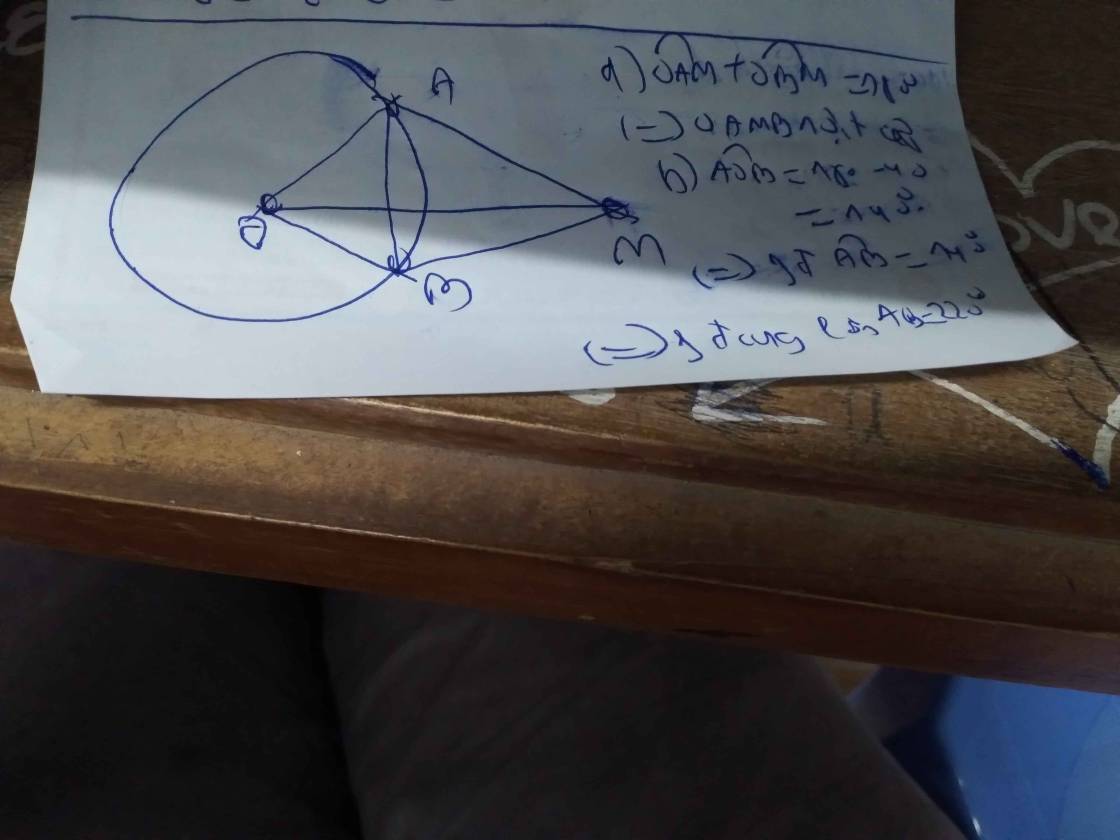
Cho (O),M là 1 điểm bên ngoài đường tròn.Vẽ tiếp tuyến MA và MB sao cho gics AMB = 70 độ.Tính góc AOB,số đo cung nhỏ và cung lớn AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
23 tháng 2 2022
giải b2:
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c,\(\widehat{PMH}=\widehat{MBH}\Rightarrow\widehat{PQH}=\widehat{O_2QP}\) => PQ là tiếp tuyến của \(\left(O_2\right)\)
Tương tự PQ cũng là tiếp tuyến \(\left(O_1\right)\)
18 tháng 3 2023
a: Xét ΔOAM vuông tại A có cosAOM=OA/OM=1/2
nên góc AOM=60 độ
=>sđ cung ANB=gócAOB=2*60=120 độ
b: góc AOB=180-36=144 độ
CM
17 tháng 10 2018
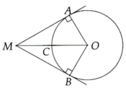
a, Sử dụng tỉ số lượng giác trong tam giác vuông ∆AMO ta tính được A O M ^ = 60 0
b, Tính được A O B ^ = 120 0 , sđ A B C ⏜ = 120 0
c, Ta có A O C ⏜ = B O C ⏜ => A C ⏜ = B C ⏜
16 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔAMB cân tại M
hay \(\widehat{AMB}=60^0\)
nên ΔAMB đều
b: Xét (O) có
NA là tiếp tuyến
NC là tiếp tuyến
Do đó: ON là tia phân giác của góc AOC(1)
Xét (O) có
QC là tiếp tuyến
QB là tiếp tuyến
Do đó: OQ là tia phân giác của góc NOB(2)
Từ (1) và (2) suy ra \(\widehat{NOQ}=\dfrac{1}{2}\cdot120^0=60^0\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
8 tháng 4 2020
Câu a:
Xét tg vuông AOB có BO=R=OA/2 => ^OAB=30 (góc đối diện với cạnh góc vuông băng nửa cạnh huyền thì bằng 30)
=> ^AOB=90-^OAB=90-30=60
Tương tj c/m đươc ^AOC=60
Câu b:
Từ câu a => ^BOC=^AOB+^AOC=120 => sđ cung BC nhỏ = 120 (sđ góc ở tâm = sđ cung chắn)
=> sđ cung BC lớn = 360-sđ cung BC nhỏ = 360-120=240