Hàm số y=(2m-1)x+2 có đồ thị là đường thẳng d.
Tìm m để khoảng cách từ gốc tọa độ đến d bằng 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2023
a: Thay x=1 và y=2 vào y=(m-1)x+4, ta được:
1(m-1)+4=2
=>m-1+4=2
=>m+3=2
=>m=-1
b:
(d): y=(m-1)x+4
=>(m-1)x-y+4=0
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+4\right|}{\sqrt{\left(m-1\right)^2+1}}=\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}\)
Để d(O;(d))=2 thì \(\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}=2\)
=>\(\sqrt{\left(m-1\right)^2+1}=2\)
=>\(\left(m-1\right)^2+1=4\)
=>\(\left(m-1\right)^2=3\)
=>\(m-1=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}+1\)
NV
12 tháng 3 2023
- Gọi M(x0,y0) ,N(x1,y1) lần lượt là giao điểm của đường thẳng (d): \(y=\left(2m-3\right)x-1\) với trục tung, trục hoành \(\Rightarrow x_0=y_1=0\).
Vì M(0;y0) thuộc (d) nên: \(y_0=\left(2m-3\right).0-1=-1\)
\(\Rightarrow M\left(0;-1\right)\) nên \(OM=1\) (đvđd)
\(N\left(x_1;0\right)\) thuộc (d) nên: \(\left(2m-3\right)x_1-1=0\Rightarrow x_1=\dfrac{1}{2m-3}\)
\(\Rightarrow N\left(\dfrac{1}{2m-3};0\right)\) nên \(ON=\dfrac{1}{2m-3}\) (đvđd)
*Hạ OH vuông góc với (d) tại H \(\Rightarrow OH=\dfrac{1}{\sqrt{5}}\)
Xét △OMN vuông tại O có OH là đường cao.
\(\Rightarrow\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{1}{OH^2}\)
\(\Rightarrow1+\left(2m-3\right)^2=5\)
\(\Rightarrow2m-3=\pm2\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)
5 tháng 12 2023
a: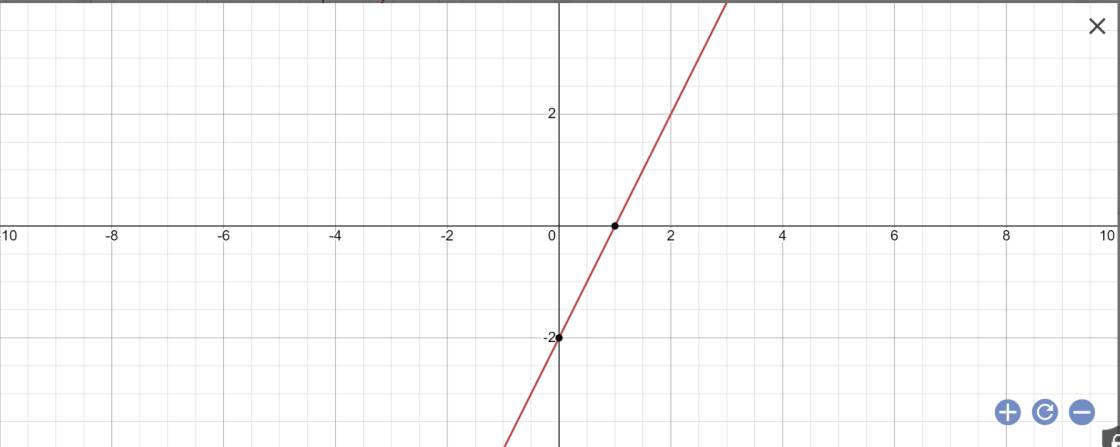 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
8 tháng 12 2023
c: y=(m-1)x+4
=>\(\left(m-1\right)x-y+4=0\)
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+4\right|}{\sqrt{\left(m-1\right)^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}\)
Để \(d\left(O;\left(d\right)\right)=2\) thì \(\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}=2\)
=>\(\sqrt{\left(m-1\right)^2+1}=2\)
=>\(\left(m-1\right)^2+1=4\)
=>\(\left(m-1\right)^2=3\)
=>\(m-1=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}+1\)
11 tháng 12 2015
m Khác 1 ( h/s ố không qua O )
+ x =0 => y = m -1 A(0;m-1)
+y =0 => x =1-m B(1-m;0)
Áp dụng HTL trong tam gics AOB vuông tại O
\(\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\Leftrightarrow\frac{1}{\left(m-1\right)^2}+\frac{1}{\left(1-m\right)^2}=\frac{1}{\sqrt{2}^2}\)
Hay (m-1)2 =4 => /m -1/ = 2 => m =3 hoặc m =-1
24 tháng 11 2023
a: Để hàm số nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b; Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
\(\left(-1\right)\left(2m-1\right)+m-1=0\)
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
\(1\left(2m-1\right)+m-1=4\)
=>2m-1+m-1=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
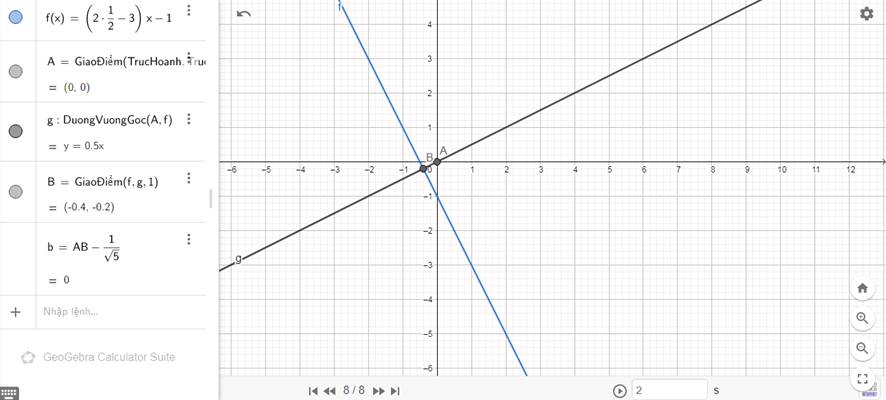
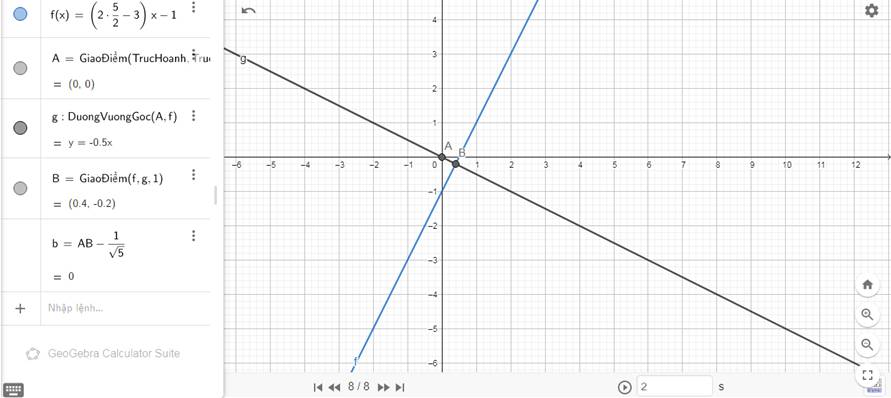
Gọi A, B lần lượt là giao điển của \(\left(d\right)\) với 2 trục \(Ox,Oy\)
Ta có : \(A\left(\dfrac{-2}{2m-1},0\right);B\left(0,2\right)\)
Gọi OH là khoảng cách từ \(\left(d\right)\) đến gốc O
Áp dụng hệ thức lượng trong tam giác vuông :
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{\left(\dfrac{-2}{2m-1}\right)^2}+\dfrac{1}{2^2}=\dfrac{\left(2m-1\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow4=\left(2m-1\right)^2+1\)
\(\Leftrightarrow4=4m^2-4m+1+1\)
\(\Leftrightarrow4m^2-4m-2=0\)
\(\Leftrightarrow2m^2-2m+1=0\)
\(\Leftrightarrow\) Ko tìm đc m
PT giao Ox và Oy:
\(\left\{{}\begin{matrix}y=0\Rightarrow x=\dfrac{2}{1-2m}\Rightarrow A\left(\dfrac{2}{1-2m};0\right)\Rightarrow OA=\dfrac{2}{\left|2m-1\right|}\\x=0\Rightarrow y=2\Rightarrow B\left(0;2\right)\Rightarrow OB=2\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến \(\left(d\right)\Rightarrow OH=1\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-1\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{\left(2m-1\right)^2+1}{4}=1\\ \Leftrightarrow\left(2m-1\right)^2+1=4\\ \Leftrightarrow\left(2m-1\right)^2=3\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{3}}{2}\\m=\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\)