tìm 3 số nguyên tố a,b,c biết ab + ba = c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
HH
2
21 tháng 6 2021
Có ab - ba là số chính phương
=> 10a + b - 10b - a là số chính phương
=> 9a - 9b là số chính phương
=> 9(a-b) là số chính phương
Mà 9 là số chính phương
=> a-b là là số chính phương
Mà 9\(\ge a>b>0\) => \(0< a-b< 9\)
=> a - b \(\in\left\{1;4\right\}\)
TH1: a - b = 1
Mà ab là số nguyên tố
=> ab = 43
TH2: a - b = 4
Mà ab là số nguyên tố
=> ab = 73
VT
11 tháng 4 2023
Có ab - ba là số chính phương
=> 10a + b - 10b - a là số chính phương
=> 9a - 9b là số chính phương
=> 9(a-b) là số chính phương
Mà 9 là số chính phương
=> a-b là là số chính phương
Mà 9≥a>b>0≥�>�>0 => 0<a−b<90<�−�<9
=> a - b ∈{1;4}∈{1;4}
TH1: a - b = 1
Mà ab là số nguyên tố
=> ab = 43
TH2: a - b = 4
Mà ab là số nguyên tố
=> ab = 73
29 tháng 10 2016
a)
p=(2,3,5,7 ...)
p^2=(4,9,25,49...)
p^2+44=(48,53,93..)
có 53 nguyên tố
ds: p=3
b).p=(6,7,8 ...)
2p+1=(13,15,17...)
4p+1=(25,29,33.....)
l25=5.5=> 4p+1 là hợp số
c)p+6=(02,03,05, ...)
p+8 =(04,05,07,....)
p+12=(08,09,11,...)
P+14=(10,11,13,...)
ds: 5,7,11,13
2.
(ab-ba)=97-79=18=2.9 loại
(ab-ba)=93-39= loại 39 ko nguyen tố
(ab-ba)=73-37=26=13.2 loại
(ab-ba)=71-17=54=9.6loại
a>=b
(ab-ba)=11-11=0
ds: ab=11
CT
1
5 tháng 11 2016
Do \(ab+1>3\)
Nên \(ab+1\) là số lẻ
Suy ra: \(a\) là số chẵn hoặc \(b\) là số chẵn
Suy ra \(a=2\) hoặc \(b=2\)
+) Khi \(a=2\)
Nếu \(b\) chia \(3\) dư \(1\) thì \(7a+b=14+b\) chia hết cho \(3\) (Loại)
Nếu \(b\) chia \(3\) dư \(2\) thì \(ab+1=2b+1\) chia hết cho \(3\) (Loại)
Vậy \(b\)chia hết cho \(3\)
Suy ra: \(b=3\)
+) Khi \(b=2\)
Cũng xét tương tự bạn nhé!
Các cặp số \(\left(a;b\right)\)) là \(\left(3;2\right)\) và \(\left(2;3\right)\)
5 tháng 11 2016
chỗ khi a = 2, nếu b chia 3 dư 2 => ab + 1 = 2b + 1 = 2.(3k + 2) + 1
= 6k + 4 + 1 = 6k + 5 chia hết cho 3 sai r`
a=2;b=5 thử lại vx đúng
18 tháng 6 2016
Trong tập hợp số nguyên không có khái niệm hai số nguyên tố cùng nhau. Trong bài này phải nói trị tuyệt đối của chúng đôi một nguyên tố cùng nhau.
PT
1
CM
24 tháng 9 2017
Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
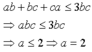
( Vì a là số nguyên tố )
Với a = 2 ta có
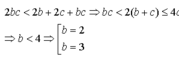
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .
18 tháng 6 2016
Không thể có \(\left|c\right|>1\) vì c có ít nhất một ước nguyên tố \(p\ge2\)
Do đó p phải là ước của a hoặc b. Vô lý vì (a;c) = ( b;c) = 1; từ đó suy ra \(c\in\left\{-1;1\right\}\)
*TH1 : \(c=-1\)
\(\Rightarrow-\left(a+b\right)=ab\)
\(\Rightarrow ab-\left[-\left(a+b\right)\right]=0\)
\(\Rightarrow ab+a+b+1=0+1\)
\(\Rightarrow\left(ab+a\right)+\left(b+1\right)=1\)
\(\Rightarrow a\left(b+1\right)+\left(b+1\right)=1\)
\(\Rightarrow\left(a+1\right)\left(b+1\right)=1\)
Do đó suy ra \(a+1=b+1=-1\) ( Chúng không thể bằng 1 vì nếu như vậy a=b=0 )
\(\Rightarrow a=b=-2\)
Do đó (a;b) = 2 \(\ne\)1 ( trái với giả thiết )
*TH2 : \(c=1\)
\(\Rightarrow a+b=ab\)
\(\Rightarrow ab-\left(a+b\right)+1=0+1=1\)
\(\Rightarrow ab-a-b+1=1\)
\(\Rightarrow\left(ab-a\right)-\left(b-1\right)=1\)
\(\Rightarrow a\left(b-1\right)-\left(b-1\right)=1\)
\(\Rightarrow\left(a-1\right)\left(b-1\right)=1\)
\(\Rightarrow a-1=b-1=1\) ( chúng không thể bằng -1 vì như vậy thì a = b = 0 )
\(\Rightarrow a=b=2\)
\(\Rightarrow\left(a;b\right)=2\ne1\) (trái với giả thiết )
Do đó không tồn tại a, b, c thỏa mãn đề bài.