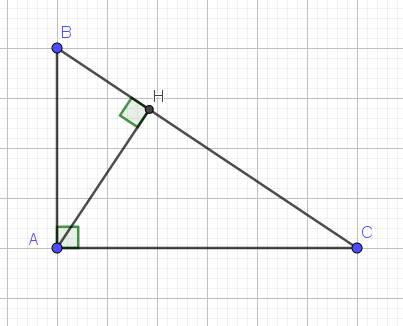
cho tam giác abc cân tại a có ac = 4,8cm; đường cao ah , m là trung điểm của cạnh ac a) tính độ dài đoạn thẳng AM b) gọi k là điểm đối xứng của h qua m tứ giác AKCH là hình gì ? vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
4 tháng 3 2018
1) TA CÓ : AB=AC ( \(\Delta ABC\)CÂN TẠI A)
AD = AE (GT)
=> AB- AE= AC- AD
=> BE = CD
XÉT \(\Delta BEC\)VÀ \(\Delta CDB\)
CÓ : BE = CD ( CMT)
\(\widehat{ABC}=\widehat{ACB}(\Delta ABC\)CÂN TẠI A)
BC LÀ CẠNH CHUNG
\(\Rightarrow\Delta BEC=\Delta CDB\left(C-G-C\right)\)
\(\Rightarrow CE=BD\)( 2 CẠNH TƯƠNG ỨNG)
2) TA CÓ: \(\Delta BEC=\Delta CDB\left(pa\right)\)
\(\Rightarrow\widehat{BEC}=\widehat{CDB}\)( 2 GÓC TƯƠNG ỨNG)
XÉT \(\Delta ACE\)VÀ \(\Delta ABD\)
CÓ: AC =AB ( \(\Delta ABC\)CÂN TẠI A)
AE = AD (GT)
CE = BD ( pa)
\(\Rightarrow\Delta ACE=\Delta ABD\left(C-C-C\right)\)
\(\Rightarrow\widehat{ACE}=\widehat{ABD}\)( 2 GÓC TƯƠNG ỨNG)
XÉT \(\Delta BEG\)VÀ \(\Delta CDG\)
CÓ: \(\widehat{BEC}=\widehat{CDB}\left(cmt\right)\)
BE = CD ( pa)
\(\widehat{ABD}=\widehat{ACE}\left(cmt\right)\)
\(\Rightarrow\Delta BEG=\Delta CDG\left(G-C-G\right)\)
\(\Rightarrow EG=DG\)( 2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\Delta GDE\)CÂN TẠI G ( ĐỊNH LÍ)
3) ( CẠNH BÊN 4,8 CM; CẠNH ĐÁY 10 CM)
CHU VI CỦA TAM GIÁC ABC LÀ:
4,8+ 4,8+ 10 = 19,6 (CM)
KL: CHU VI CỦA TAM GIÁC ABC LÀ 19,6 CM
CHÚC BN HỌC TỐT!!!!!
AH
Akai Haruma
Giáo viên
14 tháng 6 2023
Lời giải:
Áp dụng định lý Pitago:
$HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=6,4$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$BH.CH=AH^2$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{4,8^2}{6,4}=3,6$ (cm)
$BC=BH+CH=3,6+6,4=10$ (cm)
$AB=\sqrt{BC^2-AC^2}=\sqrt{10^2-8^2}=6$ (cm) - Theo định lý Pitago
8 tháng 5 2021
c) Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD=ΔHBD(cạnh huyền-góc nhọn)
8 tháng 5 2021
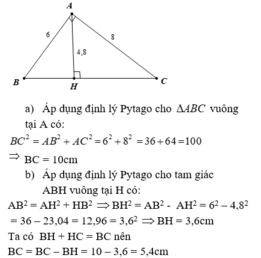
a) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
NH
0
TN
0
27 tháng 9 2021
Xét ΔAHB vuông tại H có
\(AH^2+HB^2=AB^2\)
hay AH=3,6(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\)
hay BC=7,5(cm)
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=4,5(cm)