cho tam giac ABC vuông tại A. Kẻ đường cao AH. Chứng minh rằng AH*BC = AB*AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=9,6\left(cm\right)\)
b, \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{B}\approx53^0\)
\(\Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
c, Sai đề
a. \(BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20\) (cm)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.16}{20}=9,6\) (cm)
b. \(sinB=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{B}=53^O7'\)
\(\widehat{C}=90^o-53^o7'=36^o53'\)

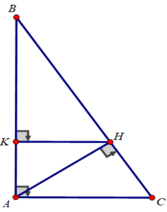
c) Xét tam giác ABC vuông tại A có ∠B = 30 0 , AC = 6 cm:
AB = AC.cotgB = 6.cotg 30 0 = 2 3 (cm)
AC = BC.sinB ⇒ 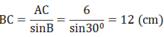
Tam giác ABC vuông tại A có AH là đường cao nên
AH.BC = AB.AC ⇒ 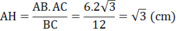

a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)

\(a,\text{Áp dụng PTG:}BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \text{Áp dụng HTL:}\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\\ b,\text{Áp dụng HTL:}\left\{{}\begin{matrix}AM\cdot AB=AH^2\\AN\cdot AC=AH^2\end{matrix}\right.\\ \Rightarrow AM\cdot AB=AN\cdot AC\)

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
b: ΔBAC đồng dạng vơi ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
c: ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{AB\cdot AC}{2}\)
Do đó: \(AH\cdot BC=AB\cdot AC\)