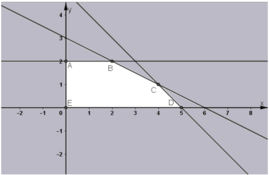
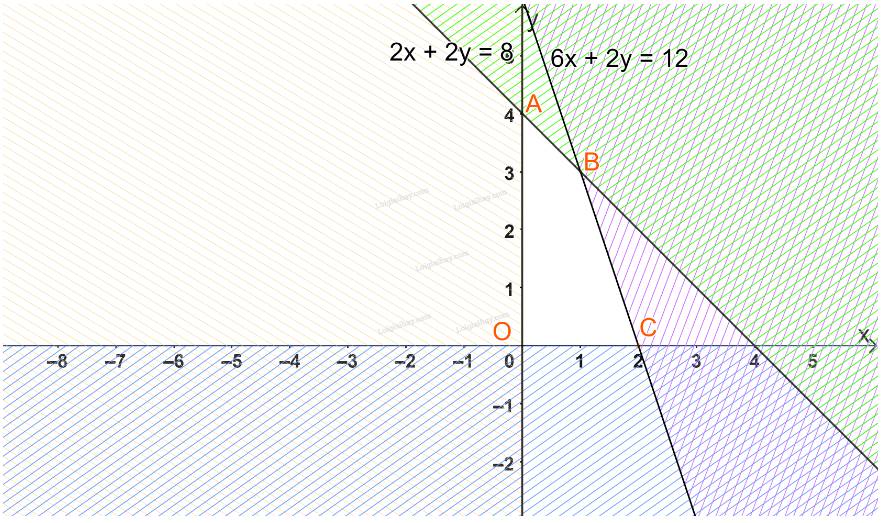
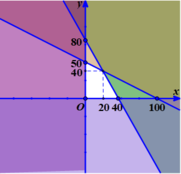
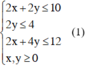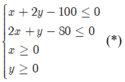Giải bài toán bằng cách lập hệ phương trình =)))))
Để sản xuất 1 máy điện loại A cần 3kg Cu và 2kg Pb, để sản xuất 1 máy điện loại B cần 2kg Cu và 1kg Pb. Sau khi sản xuất đã sử dụng hết 130kg Cu và 80kg Pb. Hỏi đã sản xuất đc bao nhiêu máy điện loại A và bao nhiêu máy điện loại B? "