Giúp em với bài này cần gấp 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
28 tháng 7 2021
lần đổ 1
\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)
\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)
\(\Leftrightarrow2mC=9m'C'\)
lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)
\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)
\(\Rightarrow t_x=...\)
12 tháng 12 2021
a)
ta có \(n_{N_2}=\dfrac{4,2}{28}=0,15\left(mol\right)\)
\(\Rightarrow V_{N_2}=0,15.22,4=3,36l\)
ta có \(n_{O_2}=\dfrac{3,2}{32}=0,1\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,1.22,4=2,24l\)
b)
ta có \(n_{SO_2}=\dfrac{32}{64}=0,5\left(mol\right)\)
\(\Rightarrow V_{SO_2}=0,5.22,4=11,2l\)
ta có \(n_{O_2}=\dfrac{32}{32}=1\left(mol\right)\)
\(\Rightarrow V_{O2}=1.22,4=22,4l\)
c)
ta có \(n_{H_2}=\dfrac{2}{2}=1\left(mol\right)\)
\(\Rightarrow V_{H_2}=1.22,4=22,4l\)
ta có \(n_{O_2}=\dfrac{8}{32}=0,25\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,25.22,4=5,6l\)
d)
ta có \(n_{N_2}=\dfrac{8,4}{28}=0,3\left(mol\right)\)
\(\Rightarrow V_{N_2}=0,3.22,4=6,72l\)
ta có \(n_{O_2}=\dfrac{6,4}{32}=0,2\left(mol\right)\)
\(\Rightarrow V_{N_2}=0,2.22,4=4,48l\)
13 tháng 1 2022
a: Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=180^0\)
Do đó: AFHE là tứ giác nội tiếp
Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=180^0\)
Do đó: BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=180^0\)
Do đó: CEHD là tứ giác nội tiếp
b: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác CDFA có
\(\widehat{CDA}=\widehat{CFA}=90^0\)
Do đó: CDFA là tứ giác nội tiếp
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó AEDB là tứ giác nội tiếp
8 tháng 9 2021
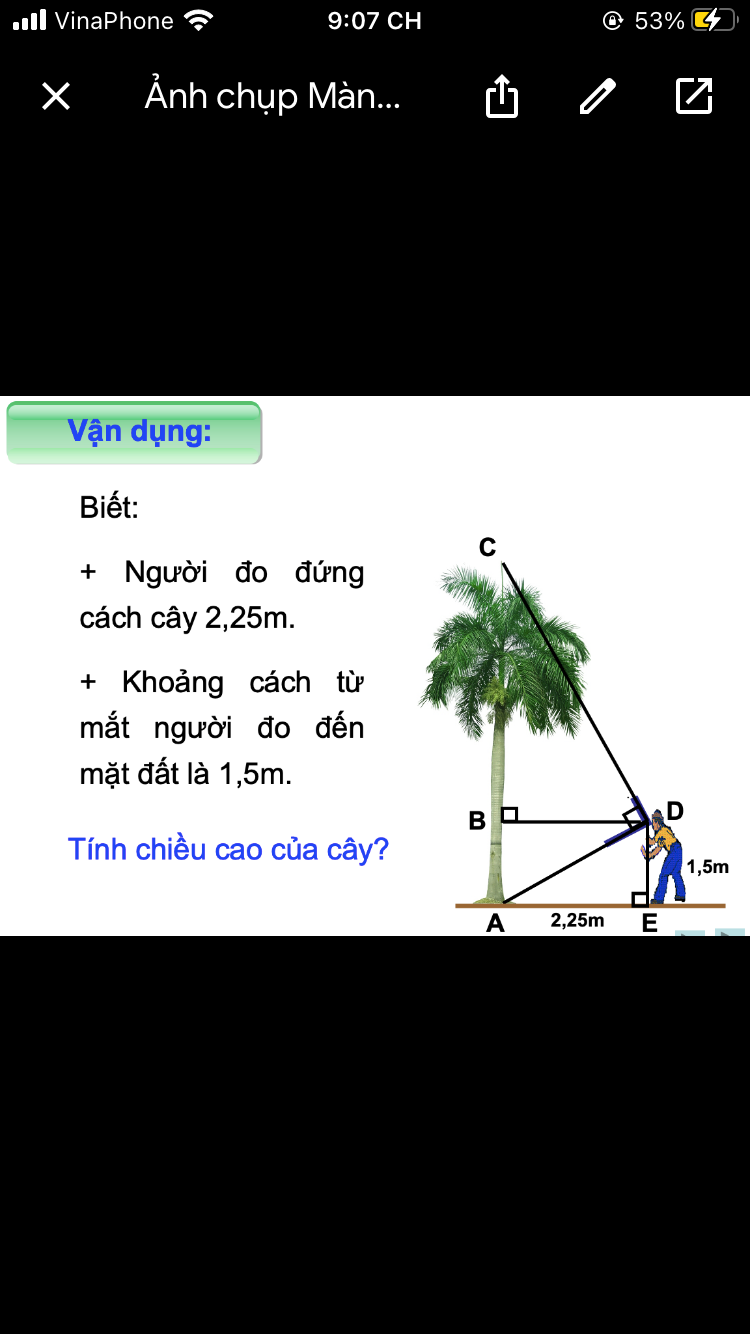
Xét tam giác ADE vuông tại E có:
\(AD^2=AE^2+DE^2\)(định lý Pytago)
\(\Rightarrow AD^2=\dfrac{117}{16}\left(m\right)\)
Xét tam giác ADC vuông tại D có đường cao DB có:
\(AD^2=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow AC=\dfrac{AD^2}{AB}=\dfrac{117}{16}:1,5=\dfrac{39}{8}\left(m\right)\)
Vậy chiều cao của cây là \(\dfrac{39}{8}m\)
Giúp em giải bài này với em đang cần gấp
Giúp em bài này với, cần gấp ạ
2
9 tháng 12 2021
a: \(\dfrac{A}{B}=\dfrac{x^3+x+3x^2+3+2}{x^2+1}=x+3+\dfrac{2}{x^2+1}\)
1 A
2 C
3 C
4 A
5 B
3C