Câu 3 (1,0 điểm) Một phòng họp có 320 ghế ngồi được xếp thành từng dãy và số ghế mỗi dãy đều bằng nhau. Nếu số dãy ghế tăng thêm 1 và số ghế mỗi dãy tăng thêm 2 thì trong phòng có 374 ghế. Hỏi trong phòng họp có bao nhiêu dãy ghế và mỗi dãy có bao nhiêu ghế ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 3 2019
Gọi số dãy ghế là x (x ∈ ℕ * ), (dãy)
Số ghế ở mỗi dãy là: 360/x (ghế)
Số dãy ghế lúc sau là x + 1 (dãy)
Số ghế ở mỗi dãy lúc sau là: 360/x + 1(ghế)
Vì sau khi tăng số dãy thêm 1 và số ghế của mỗi dãy tăng thêm 1 thì trong phòng có 400 ghế nên ta có phương trình:
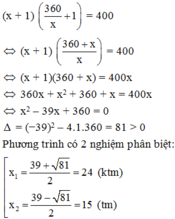
Vậy số dãy ghế là 15 (dãy)
Đáp án: B
23 tháng 5 2018
Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.
CM
26 tháng 6 2017
Gọi x (dãy) là số dãy ghế ban đầu của phòng họp.
Điều kiện: x ∈N*
Khi đó số ghế ngồi trong một dãy là: 360/x (ghế)
số dãy ghế sau khi tăng là x + 1 (dãy)
số ghế ngồi trong một dãy sau khi tăng là: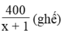
Theo đề bài, ta có phương trình: 
⇔ 400x – 360(x + 1) = x(x + 1)
⇔ 400x – 360x – 360 = x 2 + x ⇔ x 2 – 39x + 360 = 0
∆ = - 39 2 – 4.1.360 = 1521 – 1440 = 81 > 0
∆ = 81 = 9
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán.
Vậy bình thường trong phòng có 15 hoặc 24 dãy ghế.
LM
2 tháng 6 2021
Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.
9 tháng 5 2018
Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có \(\frac{240}{x}\)ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=> \(\left(\frac{240}{x}+1\right)\left(x+3\right)=315\Leftrightarrow240+\frac{720}{x}+x+3=315\)
\(\Leftrightarrow x-72+\frac{720}{x}=0\Leftrightarrow\frac{x^2-72x+720}{x}=0\Leftrightarrow x^2-72x+720=0\)
\(\Delta'=\left(-36\right)^2-720=576\)
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.
Gọi số dãy là x, số ghế là y (x;y thuộc N*)
Vì tổng số ghế là 320 nên:
xy = 320
=> y = 320/x (1)
Nếu số dãy ghế tăng tăng thêm 1 và số ghế mỗi dãy tăng thêm 2 thì trong phòng có 374 ghế nên ta có:
(x+1) (y+2) - xy = 374 - 320
=> 2x + y + 2 + xy -xy = 54
=>2x + y = 52 (2)
Thay (1) vào (2) ta có:
2x + 320/x =52
<=> 2x2x2 +320 = 52x
<=> x2x2 + 160 = 26x
<=> x2x2 - 26x +160 =0
<=> x2x2 - 10x - 16x + 160 = 0
<=> (x-16) * (x-10) = 0
<=> x = 16 hoặc x=10
=> y= 320/16 = 20 hoặc y = 320/10 =32
Vậy
TH1: Phòng họp có 16 dãy, mỗi dãy 20 chỗ
TH2: Phòng họp có 10 dãy, mỗi dãy 32 chỗ
3 con giáp là con trâu