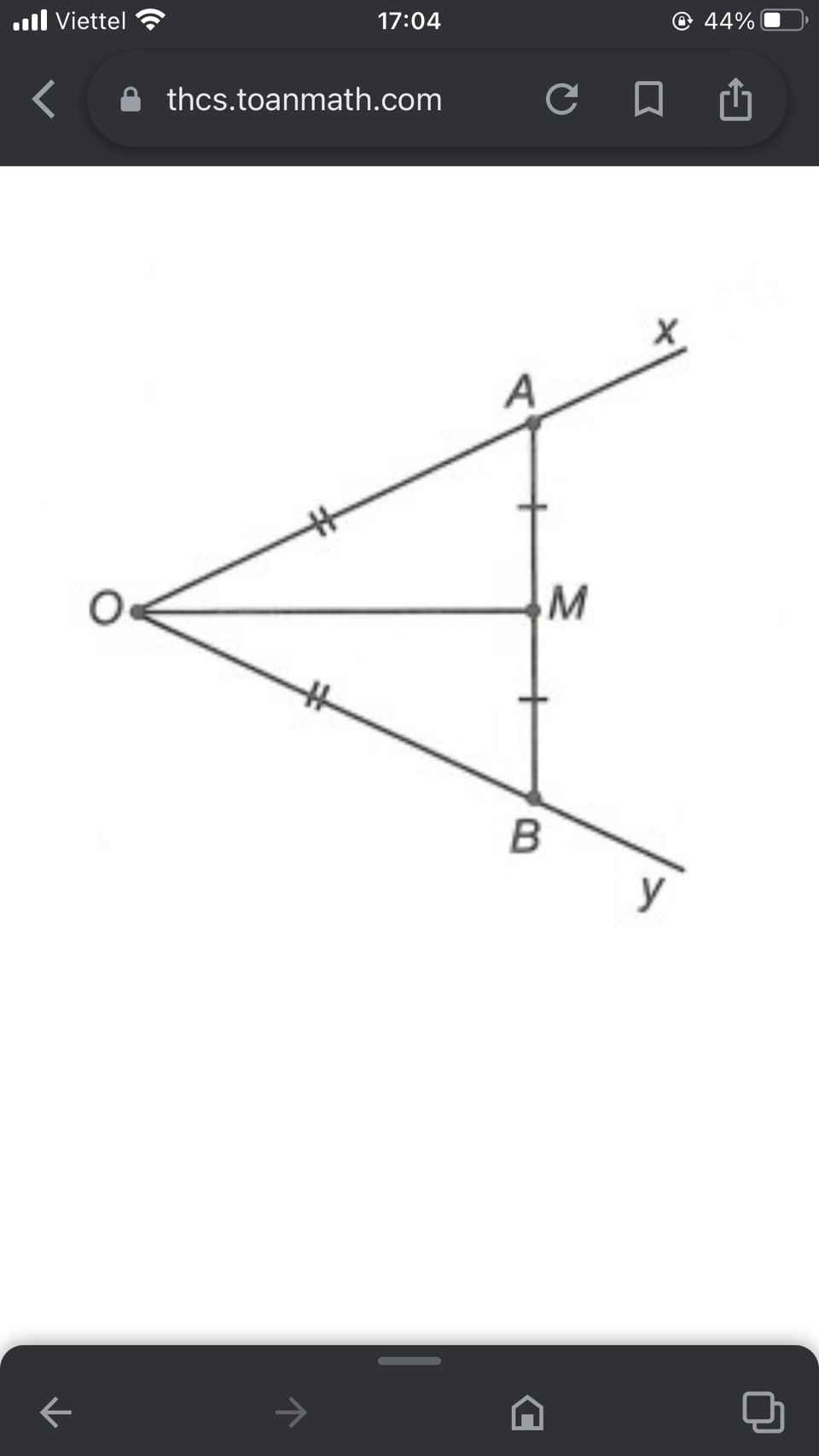
Chứng minh tam giác OAM = tam giác BOM
giúp mik với mọi người ơi mình cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2022
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
1 tháng 4 2021
Gọi tam giác đó là ΔBAC cân tại A có BM và CN là hai đường trung tuyến
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔBAC cân tại A)
nên AN=NB=AM=MC
Xét ΔAMB và ΔANC có
AM=AN(cmt)
\(\widehat{BAM}\) chung
AB=AC(ΔABC cân tại A)
Do đó: ΔAMB=ΔANC(c-g-c)
Suy ra: BM=CN(hai cạnh tương ứng)
PT
11 tháng 4 2021
a) Xét ΔDEI và ΔDFI c
DE = DF (ΔDEF cân)
DI là cạnh chung.
IE = IF (DI là trung tuyến)
➩ ΔDEI = ΔDFI (c.c.c)
b) Vì ∆DEI = ∆DFI => \(\widehat{DIE}\) \(= \widehat{DIF}\)
mà \(\widehat{DIE}\)+\(\widehat{DIF}\)=1800( kề bù)
nên \(\widehat{DIE}\)\(= \widehat{DIF}\)=900
c) I là trung điểm của EF nên IE = IF = 5cm.
ΔDIE vuông tại I
➩ DE2=DI2+EI2 (định lí Pitago)
➩ DI2=132–52=144
➩DI=12.
Xét ΔOAM và ΔBOM có:
\(OA=OB\left(gt\right)\\ AM=BM\left(gt\right)\\ ChungOM\)
⇒ΔOAM=ΔBOM(c.c.c)
xét △OAM và △BOM
ta có: OA=OB(2 cạnh tương ứng)
MA=MB(2 cạnh tương ứng)
OM là cạnh chung
=>△OAM =△BOM