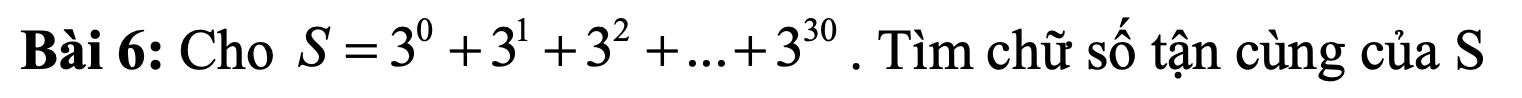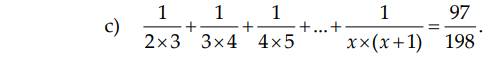Mọi người giúp mình vs nha! ai đúng và đủ thì mình tick cho.Mình đang cần gấp .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
28 tháng 3 2021
\(\frac{1}{2}+\frac{1}{5}+\frac{2}{9}\)
=\(\frac{45}{90}+\frac{18}{90}+\frac{20}{90}\)
=\(\frac{83}{90}\)
HT
1
19 tháng 8 2021
\(2S=3^{31}-1=3^{28}.3^3-1=\left(...1\right).27-1=\left(.....7\right)-1=\left(...6\right)\)
\(\Rightarrow S=\left(...3\right)\)
Tận cùng bằng 3 nhé e
19 tháng 8 2021
3^0 có tận cùng là 1.
3^1 có tận cùng là 3.
3^2 có tận cùng là 9.
3^3 có tận cùng là 7.
3^4 có tận cùng là 1.
................................
3S = ( 3^1+3^2+3^3+......+3^31 )
3S-S = ( 3^1+3^2+3^3+......+3^31 ) - ( 3^0+3^1+3^2+......+3^30 )
2S = 2^31-1
2^31 có tận cùng là 1. ( theo như công thức đã nêu trên )
=> 2S có tận cùng là 0.
2S-S = 2S : 2
=> S có tận cùng là 5 vì ....0 : 2 bằng 5.
DH
31 tháng 3 2020
Ta có b/c=3/4 nên b/3=c/4 =>b/12=c/16(1)
mà a/1=b/4=>a/3=b/12(2)
Từ (1)và (2) suy ra :
a/3=b/12=c/16=>4a/12=b/12=c/16
áp dụng tính chất dãy tỉ số bằng nhau ta có :
4a/12=b/12=c/16=4a+b-c/12+12-16=8/8=1
=>a/3=1=>a=1.3=3
=>b/12=1=>b=1.12=12
=>c/16=1=>c=1.16=16
Vậy a=3,b=12,c=16
D
31 tháng 3 2020
theo đề bài ta có :\(\frac{b}{3}=\frac{c}{4}\)và\(\frac{3}{4}=\frac{b}{c}\)
từ trên \(\Rightarrow\frac{b}{12}=\frac{c}{16}\)
\(\frac{a}{1}=\frac{b}{4}\Rightarrow\frac{a}{3}=\frac{b}{12}\)
như vậy từ đây áp dụng tính chất dãy tỉ số bằng nhau ,ta có:
\(\frac{4a}{12}=\frac{b}{12}=\frac{c}{16}=\frac{4a+b-c}{12+12-16}=\frac{8}{8}hay1\)
\(\frac{a}{3}=1\Rightarrow a=3\)
\(\frac{b}{12}=1\Rightarrow b=12\)
\(\frac{c}{16}=1\Rightarrow c=16\)
vậy ta có a=3 ; b=12 ; c=16
21 tháng 5 2022
gia đình ấp ủ bên em
làng quê vắng vẻ nhưng đầy tình thương
bạnviết tạm đi để mình nghĩ
KN
6 tháng 8 2019
*Vẽ các trung tuyến BN, CE lần lượt tại B và C. Gọi G là trọng tâm của \(\Delta ABC\)..Nối MN
Áp dụng BĐT tam giác vào \(\Delta AMN\), ta được:
\(AM< AN+NM\)(1)
Mà \(AN=\frac{1}{2}AC\)(Do BN là trung tuyến ứng với cạnh AC) (2)
và \(MN=\frac{1}{2}AB\)(Do MN là đường trung bình ứng với cạnh \(AB\)của \(\Delta ABC\)) (3)
Từ (1), (2) và (3) suy ra \(AM< \frac{1}{2}AB+\frac{1}{2}AC\)
hay \(AM< \frac{1}{2}\left(AB+AC\right)\) (đpcm)
