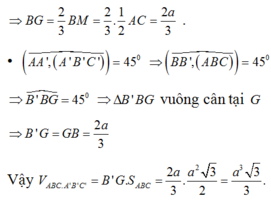cho lăng trụ đứng ABC. A'B'C' có đáy là tam giác ABC vuông tại A có AB=6, BC=10, AA'=5. Tính thể tích hình lăng trụ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AC=\sqrt{10^2-6^2}=8\)
S đáy=1/2*6*8=3*8=24
V=24*5=120

Đáp án D
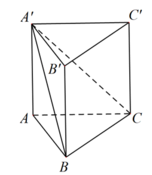
A ' B C , A B C = A ' B A ^ = 30 0 .
A A ' = A B . t a n 30 0 = a 3 3 .
S A B C = 1 2 B A . B C = a 2 2 2 .
V A B C = A A ' . S A B C = a 3 3 ⋅ a 2 2 2 = a 3 6 6 .

Đáp án D
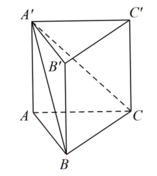
A ' B C , A B C = A ' B A ^ = 30 0 .
A A ' = A B . t a n 30 0 = a 3 3 .
S A B C = 1 2 B A . B C = a 2 2 2 .
V A B C = A A ' . S A B C = a 3 3 ⋅ a 2 2 2 = a 3 6 6 .

Đáp án A
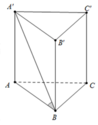
Ta có: S đ = B C 2 2 = a 2 2 Do A'B tạo (ABC) với một góc 60 ∘ nên A ' B A ⏜ = 60 ∘
Do đó
AA ' = A B tan 60 ∘ = a 3 ⇒ V A B C . A ' B ' C ' = S đ h = a 3 3 2 .

Lời giải:
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-16^2}=12$ (cm)
Diện tích đáy là: $(12.16):2=96$ (cm2)
Diện tích toàn phần:
$S=p_{đáy}.h+2S_{đáy}=(16+12+20).12+2.96=768$ (cm2)
Thể tích lăng trụ:
$V=S_{đáy}.h=96.12=1152$ (cm3)

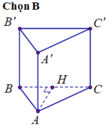
Ta có AA’//(BCC’B’) nên khoảng cách từ AA' đến mặt phẳng (BCC'B') cũng chính là khoảng cách từ A đến mặt phẳng (BCC'B').