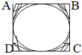
Cho hình vuông ABCD có hai đường chéo AC và BD vuông góc với nhau và bằng 12cm.Hai đ]ơngf chéo này cắt nhau ở O.Từ O ta vẽ một hình tròn có đường kính bằng cạnh hunhf vuông ABCD.Tính diện tích hình tròn này?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 6 2018
a) Vẽ hình vuông ABCD có cạnh 5cm. Nối đỉnh A với đỉnh C, đỉnh B với đỉnh D.
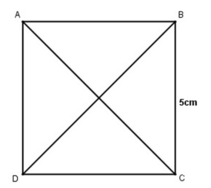
b) Kiểm tra rồi viết (Đ) đúng, (S) sai vào ô trống
| - Hai đường chéo AC và BD vuông góc với nhau | Đ |
| - Hai đường chéo AC và BD không vuông góc với nhau | S |
| - Hai đường chéo AC và BD bằng nhau | Đ |
| - Hai đường chéo AC và BD không bằng nhau | S |
DD
Đoàn Đức Hà
Giáo viên
8 tháng 7 2021
Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
DD
Đoàn Đức Hà
Giáo viên
8 tháng 7 2021
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),
CM
8 tháng 1 2019
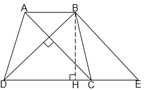
Qua B vẽ đường thẳng song song với AC, cắt DC ở E. Gọi BH là đường cao của hình thang. Ta có BE // AC, AC ⊥ BD nên BE ⊥ BD
Áp dụng định lý Pytago vào tam giác vuông BDH, ta có: B H 2 + H C 2 = B D 2
12 2 + H D 2 = 15 2 ⇒ H D 2 = 81 => HD = 9cm
Xét tam giác BDE vuông tại B:
B D 2 = D E . D H ⇒ 15 2 = D E . 9 ⇒ D E = 25 c m DE = 25cm
Ta có: AB = CE nên AB + CD = CE + CD = DE = 25cm
Do đó S A B C D = 25.12 : 2 = 150( c m 2 )
Đáp án cần chọn là: A