1GIẢI hệ phương trình căn x + trị tuyệt đối của y+1 = 5 và x*(y bình phương + 2y +1)=36
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xin lỗi ạ. Tại không giỏi đánh máy. Vậy bỏ câu này đi ạ. Chị giải câu kia giúp e nhé

Em nên chèn bằng công thức nhé, chứ em viết thế này cô không hiểu đúng đề bài em cần được để trợ giúp em đâu

Để hệ phương trình a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5 có nghiệm là (x; y) = (3; -1) thì (x;y) = (3; -1) thỏa mãn hệ phương trình
Thay x = 3, y = -1 vào hệ phương trình ta được:
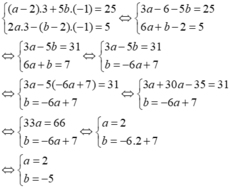
Vậy với a = 2, b = -5 thì hệ phương trình a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5 có nghiệm là (x;y) = (3; -1)

Ta có: D = 2 − 1 1 2 = 5 ≠ 0
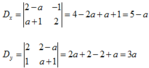
Vì D ≠ 0 nên hệ phương trình có nghiệm duy nhất
x = D x D = 5 − a 5 ; y = D y D = 3 a 5
Khi đó:
x 2 + y 2 = 5 − a 5 2 + 3 a 5 2
= 25 − 10 a + 10 a 2 25 = 10 25 a 2 − a + 1 = 2 5 a − 1 2 2 + 9 10 ≥ 9 10
Dấu “=” xảy ra ⇔ a = 1 2
Đáp án cần chọn là: C

a) Thay m=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}3x+y=7\\x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=2\\x+y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\)
Vậy: Khi m=-1 thì (x,y)=(1;4)
b) Ta có: \(\left\{{}\begin{matrix}3x+y=2m+9\\x+y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+y=2m+9\\x=5-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(5-y\right)+y=2m+9\\x=5-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15-3y+y=2m+9\\x=5-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=2m-6\\x=5-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-m+3\\x=5-\left(-m+3\right)=5+m-3=m+2\end{matrix}\right.\)
Ta có: \(x^2+2y^2=18\)
\(\Leftrightarrow\left(m+2\right)^2+2\cdot\left(-m+3\right)^2=18\)
\(\Leftrightarrow m^2+4m+4+2\left(m^2-6m+9\right)-18=0\)
\(\Leftrightarrow m^2+4m-14+2m^2-12m+18=0\)
\(\Leftrightarrow3m^2-8m+4=0\)
\(\Leftrightarrow3m^2-2m-6m+4=0\)
\(\Leftrightarrow m\left(3m-2\right)-2\left(3m-2\right)=0\)
\(\Leftrightarrow\left(3m-2\right)\left(m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3m-2=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3m=2\\m=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{2}{3}\\m=2\end{matrix}\right.\)

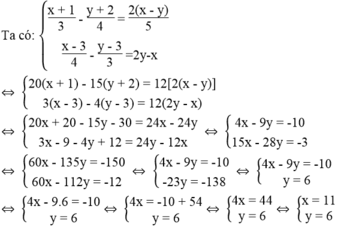
Vì (x; y) = (11; 6) là nghiệm của phương trình 3mx – 5y = 2m +1 nên ta có:
3m.11 – 5.6 = 2m + 1
⇔ 33m – 30 = 2m + 1 ⇔ 31m = 31 ⇔ m = 1
Vậy với m = 1 thì nghiệm của x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.