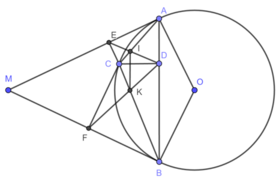
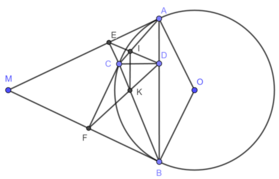
Từ điểm M nằm ngoài (O) vẽ 2 tiếp tuyến MA,MB.Trên cung nhỏ AB lấy C.vẽ CD,CE,CF lần lượt vuông góc vs AB,AM,BM.Gọi I là giao điểm của AC với DE, K là giao điểm BC với DF.C/m DC2=CE.CF và IK vuông góc với CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
13 tháng 2 2016
Hình tự vẻ tui chỉ hướng sơ qua thôi nha
Đầu tiên bà c/m tứ giác AECD và tứ giác BFCD nội tiếp (dựa vào tổng 2 góc đối)
*tứ giác AECD nội tiếp => ECD+EAD=180 độ
*tứ giác BFCD nội tiếp =>FCD+FBD =180 độ
Mà EAD=FBD (cùng chắn cung AB)
=>ECD=FCD (dc 1 cặp)
Vì B,D,C,F cùng thuộc 1 dtron và CDF ; FBC cùng nhìn CF
=>CDF=FBC
tượng tự ta cũng c/m dc CED=CAB
Mà CAB=FBC (cùng chắn cung BC)
=>2 góc kia = nhau
Đến đó dc 2 cặp rồi c/m 2 tam giác đồng dạng xong 1 nốt còn một cái nữa. (mời quý vị đừng rời mắc khỏi màn hình)
Rồi bây giờ c/m vuông góc
Ta có : CAB=CDK (dựa vào mấy cái góc = nhau đã chứng minh ở trên)
Ta lại có 2 tam giác đồng dạng vừa c/m xong
=>IDC=CFD
=>IDC=CBA (CBA=CFD)
suy ra: IDC+CDK=CAB+CBA=180 độ - ICK
=>IDC+CDK+ICK=180 độ
=>IDK + ICK=180 độ
=>tứ giác UCKD nội tiếp
hay I,C,K,D cùng thuộc 1 dtron
Mà CIK và CDK cùng nhìn CK
=>2 góc đó = nhau
Mà CDK=CAB
=>CIK=CAB
=>IK//AB (đồng vị )
=>IK vuông góc CD
CM
13 tháng 8 2019
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)
CM
18 tháng 5 2019
( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)
7 tháng 6 2020
gọi G là giao của tia đối tia CD với AM (ta giả sử cung AC < cung BC)
ý c: từ b suy ra tam giác CDE đồng dạng CFD
=> \(\widehat{ECD}=\widehat{FCD}\)
ta có: \(\widehat{ECD}+\widehat{GCE}=180^o\)
\(\widehat{FCD}+\widehat{GCF}=180^o\)
\(\widehat{GCE}=\widehat{GCF}\)suy ra đccm
ý d: CM IK//AB
Ta có: \(\widehat{FDB}=\widehat{FCB}\)(BDCF nôi tiếp đường tròn)
\(\hept{\begin{cases}\widehat{FCB}+\widehat{FBC}=90^o\\\widehat{DCA}+\widehat{CAD}=90^o\end{cases}}\)
mà \(\widehat{CAD}=\widehat{FBC}\)(cùng chắn cung BC)
\(\Rightarrow\widehat{FCB}=\widehat{DCA}\Rightarrow\widehat{FDB}=\widehat{DCA}\)(1)
Tương tự:
\(\hept{\begin{cases}\widehat{ECA}+\widehat{EAC}=90^o\\\widehat{DCB}+\widehat{DBC}=90^o\end{cases}}\)
mà \(\widehat{EAC}=\widehat{DBC}\)(cùng chắn cung AC)
\(\Rightarrow\widehat{ECA}=\widehat{DCB}\). mà \(\widehat{ECA}=\widehat{EDA}\)(tứ giác ECDA nội tiếp nên 2 góc kia cùng chắn cung AE)
\(\Rightarrow\widehat{DCB}=\widehat{EDA}\)(2)
(1)+(2) => \(\widehat{ACD}+\widehat{BCD}=\widehat{FDB}+\widehat{EDA}\)
\(\Rightarrow\widehat{ICK}=\widehat{FDB}+\widehat{EDA}\)\(\Rightarrow\widehat{ICK}+\widehat{IDK}=\widehat{FDB}+\widehat{EDA}+\widehat{IDK}=180^o\)
suy ra tứ giác IDKC nội tiếp \(\Rightarrow\widehat{CKI}=\widehat{CDI}=\widehat{CAE}=\widehat{CBA}\)
mà góc CKI và góc CBA ở vị trí đồng vị suy ra IK//AB. ta đc đccm.
Bài 5:Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA,
MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD AB, CE
MA, CF MB.
Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng
minh rằng:
a) Các tứ giác AECD, BFCD nội tiếp được.
b) CD2 = CE. CF
c)* IK // AB
Trước tiên, đề của bạn có lẽ sai hai chỗ: I là giao điểm của AC và DE chứ không phải là DF, và thứ 2 nữa là CD^2 thông thể bằng DE.DF, bạn xem lại nhe!
Câu 1. Dễ thấy AECD và BFCD nội tiếp.
Câu 2. Ta sẽ chứng minh tgCED và tgCDF đồng dạng.
Thật vậy:
Vì MA, MB là các tiếp tuyến của (O) nên ^MAB = ^MBA (1)
Mà ^ECD + ^MAB = 180; ^DCF + ^MBA = 180 (các góc đối của tứ giác nội tiếp) nên ^ECD = ^DCF (*)
Có ^EDC = ^CAE (hai góc nội tiếp cùng chắn mộ cung - trong đường tròn ngoại tiếp AECD)
^CAE = ^ABC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cùng chắn cung - đtròn O)
^ABC = ^DFC (hai góc nội tiếp cùng chắn mộ cung - trong đường tròn ngoại tiếp BFCD)
=> ^ECD = ^DFC (**)
(*) (**) => tgCED và tgCDF đồng dạng.
=> CE/CD = CD/CF => CD^2 = CE.CF.
(CD^2 không thể bằng DE.DF vì trong các tam giác DEC, DCF thì DE, DF là lớn nhất, lớn hơn CE, CF (do các cạnh đó đối diện với góc tù trong tam giác - bạn tự suy nghĩ xem tại sao các góc ECD, FCD là góc tù nhe!) nên DE.DF > CE.CF!)
Câu 3. Trong tam giác vuông DCB có ^ABC + ^DCB = 90 mà ^EDC = ^ABC (cm câu 2)
=> ^EDC + ^DCK = 90
Chứng minh tương tự ta cũng có ^CDK + ^DCI = 90
=> ^EDC + ^DCK + ^CDK + ^DCI = 180 hay ^IDK + ^ICK = 180 => DICK nội tiếp.
Câu 4.Có ^EDC + ^DCK = 90 (cm câu 3)
mà ^DIK = ^DCK (Hai góc nội tiếp cùng chắn cung - trong đường tròn ngoại tiếp DICK)
=> ^EDC +^ DIK = 90 => ^IHD = 90 (H là giao điểm của IK và CD)
=> IK vuông góc CD => IK // AB (vì AB cũng vuông góc với CD).